2020-05-11
74
| Задания | Достаточные знания | Формула |
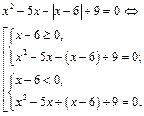
| Определение модуля числа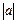 
| 
|
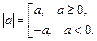
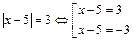
| Свойство равносильности уравнений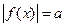 
| 
|
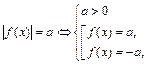
| Свойство равносильности уравнений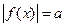
| 
|
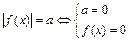
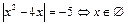
| Свойство равносильности уравнений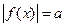
| 
|
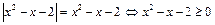
| Свойство равносильности уравнений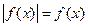 
| 
|
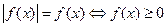
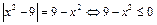
| Свойство равносильности уравнений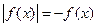 
| 
|
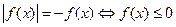
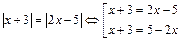
| Свойство равносильности уравнений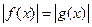 
| 
|
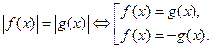
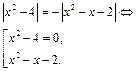
| Свойство равносильности уравнений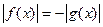 
| 
|
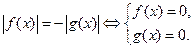
Примерное задание.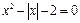 
Решение: Введем замену 
, тогда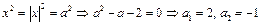 
- корни уравнения. Вернемся к замене 
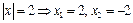и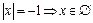 
.
Ответ: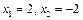 
Для решения используем последовательно знания следующих свойств:
ü Метод решения уравнений: введение новой переменной.
ü Свойство модуля :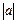 
.
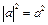ü Решения квадратного уравнения.
ü Определение модуля :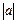 
.
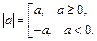ü Свойство равносильности уравнений :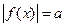 
.
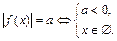Примеры иррациональных уравнений и достаточные знания свойств, необходимые для решения этих заданий.
| Задания | Достаточные знания свойств | Формула |
| Свойство корня n -ой степени 
| 
|
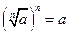
| Свойство корня четной степени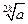 
| 
|
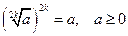
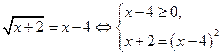
| Свойство равносильности иррациональных уравнений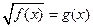 
| 
|
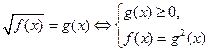
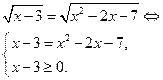
| Свойство равносильности иррациональных уравнений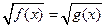 
| 
|
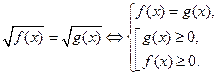
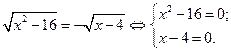
| Свойство равносильности иррациональных уравнений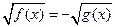 
| 
|
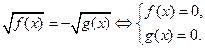
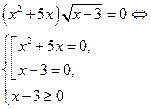
| Свойство равносильности иррациональных уравнений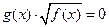 
| 
|
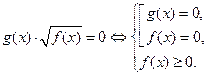
Примерное задание. Решите уравнение 
Решение.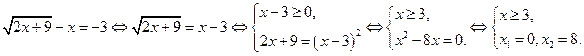 
Ответ.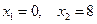 
Для решения используем последовательно знания следующих свойств:
ü Свойство равносильности иррациональных уравнений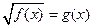 
: 
.
ü Формулы сокращенного умножения: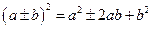 
.
ü Решение неполных квадратных уравнений.
«Показательные и логарифмические уравнения»
Теоретический справочник
Решение показательных и логарифмических уравнений основывается на теореме:
на множестве E, если для любого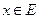 
функция f монотонна на множестве 
.
