2020-05-11
88
Задание №1. Решить уравнение 
Образец решения: 
Ответ: 
.
Для решения используем следующие знания:
ü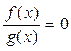 
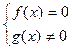
ü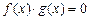 
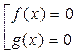
Задание №2. Решить уравнение 
Образец решения: Коэффициент при старшей степени равен 1, поэтому целые корни уравнения надо искать среди делителей свободного члена: 
1; 2; 3; 4; 6; 12. используя схему Горнера, найдем целые корни уравнения:
| 1 | -1 | -8 | 12 | ||
| 1 | 0 | -8 | 4 | не корень |
| 1 | -2 | -6 | 18 | не корень |
| 1 | 1 | -6 | 0 | корень |
Ответ: 
.
Для решения используем следующие знания:
ü Теоремы, используемые для решения уравнений высших степеней
ü Схема Горнера, для отыскания корня уравнения высших степеней
ü 
Задание №3. Решить уравнение 
. Найти целые корни.
Образец решения: Для успешного решения такого уравнения надо раскрыть скобки в парах, так чтобы выражения с переменной были похожи:
а) Если 
и 
, товыражения с переменной совсем не похожи;
в) Если 
и 
, товыражения с переменной можно считать похожими.
Тогда 
. Так как 
не является корнем уравнения, то можно разделить на 
, получим 
. Введем новую переменную 
. Уравнение примет вид 
. Вернемся к замене 
Ответ: 
.
Для решения используем следующие знания:
ü Стандартные приемы: раскрытие скобок.
ü Методы решения уравнений: введение новой переменной.
ü Правила преобразования уравнений.
ü Решение квадратного уравнения.
Задание №4. Решить уравнение 
Образец решения: Сгруппируем слагаемые 
. Введем новую переменную 
, тогда 
. Уравнение примет вид 
. Вернемся к замене 
Ответ: 
.
Для решения используем следующие знания:
ü Стандартные приемы: группировка слагаемых.
ü Методы решения уравнений: введение новой переменной.
ü Решения квадратного уравнения.
«Уравнения с модулем. Иррациональные уравнения»
Теоретический справочник
Уравнения с модулем
При решении уравнений, содержащих неизвестную под знаком модуля, в соответствии с правилом раскрытия модуля, рассматриваются два случая: выражение под знаком модуля отрицательно и неотрицательно.
· 
· 
· 
· 
Уравнения вида 
, содержащие алгебраическую сумму двух и более модулей, решают методом промежутков:
- определяют область допустимых значений неизвестной x;
- находят значения неизвестной x 1, x 2, x 3, …, xn , при которых выражения, стоящие под знаком модуля, обращаются в 0;
- наносят все xi из ОДЗ на числовую прямую, разделив ее на i + 1 промежутков;
- на каждом из i + 1 промежутков раскрывают каждый модуль по правилу раскрытия модуля;
- решают i + 1 уравнения, в ответ выписывают объединение всех решений уравнений.
