Образцы решения заданий по теме «Показательные уравнения»

Задание №1. Решить уравнение

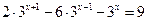
Образец решения: Так как 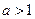, то за скобки выносим степень с наименьшим показателем

Ответ: .

Для решения используем следующие знания:

ü Свойство показательной функции: если 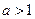, то 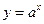- возрастающая.

ü Свойство частного степеней с одинаковыми основаниями: .

ü Свойство степени с нулевым показателем: .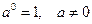

Задание №2. Решить уравнение

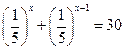
Образец решения: Так как , то за скобки выносим степень с наибольшим показателем

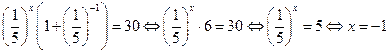
Ответ: .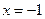

Для решения используем следующие знания:

ü Свойство показательной функции: если , то 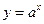- убывающая.

ü Свойство частного степеней с одинаковыми основаниями: .

ü Свойство степени с отрицательным показателем: .

Примеры заданий логарифмических уравнений и достаточные знания, необходимые для решения этих заданий.

Задания	Достаточные знания	Формула
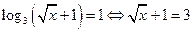
	Определение логарифма
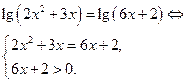
	Свойство равносильности логарифмических уравнений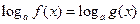
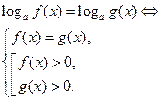
	Свойство равносильности логарифмических уравнений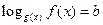
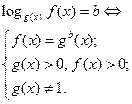
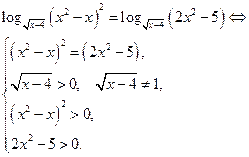
	Свойство равносильности логарифмических уравнений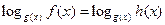

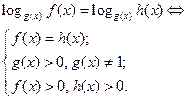
Примерное задание. Решите уравнение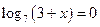

Решение: .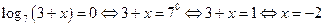

Ответ: .

Для решения используем последовательно знания следующих свойств:

ü Свойство логарифма числа : .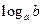

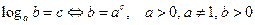ü Свойство степени с нулевым показателем: .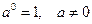

ü Свойство равносильности уравнени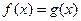й  и : .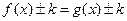

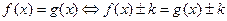Образцы решения заданий по теме «Логарифмические уравнения».

Задание №1. Решить уравнение

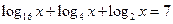
Образец решения: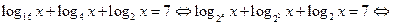

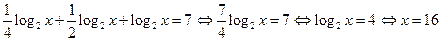
Ответ: .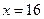

Для решения используем следующие знания:

ü Свойство логарифма : .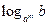

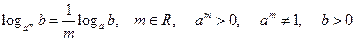ü Определение логарифма: .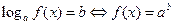

Задание №2. Решить уравнение

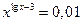
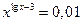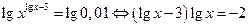Образец решения: Прологарифмируем обе части уравнения ,   по основанию 10 . Пусть , тогда 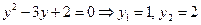. Вернемся к замене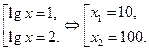

Ответ: .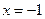

Для решения используем следующие знания:

ü Метод логарифмирования: .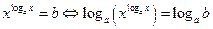

ü Свойство логарифма : .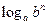

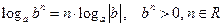ü Метод замены переменной.

ü Решение квадратного уравнения.

ü Определение логарифма: .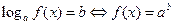

 «Тригонометрические уравнения»