Учебная КАРТА практического занятия №9

 

Дата	Группа
	1111
	1211
	1311
	1411
	1511

Наименование учебной дисциплины

ОУДП.12 Математика

Наименование темы учебной дисциплины Тема 3.1: Прямые и плоскости в пространстве.

Тема практического занятия: Решение задач на нахождение расстояния: от точки до плоскости, от прямой до плоскости, между параллельными плоскостями, между скрещивающимися прямыми

Количество часов: 2часа   

Место проведения:  Кабинет Математики

Характер работы:  репродуктивный

Форма организации учебной деятельности студентов: индивидуальная

Образовательные задачи:

1)Обобщение, закрепление теоретических знаний:

- Определения: расстояние от точки до плоскости,расстояние между скрещивающимися прямыми, расстояние между параллельными плоскостями,

- различные методы нахождения расстояния от точки до плоскости: используя определение, метод объемов, геометрический, алгебраический,координатный метод, векторный метод, семь способов нахождения расстояния между скрещивающимися прямыми.

 2) Формирование умений:

- на примере одной задачи рассмотрены различные методы нахождения расстояния от точки до плоскости, решению практических задач, которые встречаются в заданиях С₂ ЕГЭ по математике.

3) Формирование интеллектуальных и исследовательских умений:

- выделять главное, существенные признаки;

- осуществлять самоконтроль и коррекцию своей учебной деятельности;

- рационально использовать рабочее время.

4) Формирование компонентов компетенций

- владение основами научной организации труда;

- способность к самостоятельному поиску истины.

Оборудование (аппаратура, материалы и др.):

– раздаточный материал, тексты заданий;

- ПК и медиаоборудование;

- компьютерная презентации в среде Power Point

                                                            

Задание студентам на самоподготовку (учебная и справочная литература):

М.И. Башмаков, Задачник по математике Гл.3, п.3.53-3.64, с. 57-58

Башмаков М.И., Сборник задач профильной направленности,

Часть 1, глава 3, с.19-23

 

Хронологическая структура заданий практического занятия

Время (мин)	5	10	15	20	25	30	35	40	45	50	55	60	65	70	75	80	85	90
Структурные элементы	1	2	2	2	3	3	3	4	4	4	4	4	4	4	4	4	5	5

ДИДАКТИЧЕСКАЯ СТРУКТУРА ЗАНЯТИЯ

Структурные элементы	Деятельность преподавателя	Деятельность студентов
1. Целевая установка.	1. Сообщение плана учебного занятия. 2. Ознакомление с требованиями к знаниям и умениям по теме.	1. Подготовка рабочего места 2. Запись темы урока.
2. Проверка теоретической готовности студентов к выполнению заданий практического занятия	Проверка домашнего задания: 1) проверка выполнения решения задач №№…. (в рабочих тетрадях) 2) организация фронтального опроса 3) организация индивидуального опроса (у доски) – решение типовой задачи с объяснением алгоритма действий	Демонстрируют выполнение домашнего письменного задания Отвечают на вопросы Решают задачу. Объясняют алгоритм решения
3. Инструктаж о содержании, этапах работы, способах (методах) действий.	1) Сообщение содержания и последовательности выполнения практических заданий 2) Представление комплектов материалов, необходимых для выполнения заданий (учебник, компьютерная презентация, раздаточный материал) 3) Обучение практическим приемам:       Определения: расстояние от точки до плоскости,расстояние между скрещивающимися прямыми, расстояние между параллельными плоскостями,	1) Подготовка к выполнению практических заданий 2) Ознакомление с комплектом учебных материалов 3) Усвоение правил работы:  на примере одной задачи рассмотрены различные методы нахождения расстояния от точки до плоскости
4. Организация выполнения заданий практического занятия	1) Организация выполнения студентами практических заданий:  Решение задач на нахождение расстояния от точки до плоскости	Самостоятельная работа студентов по выполнению заданий
5. Оценка выполненной работы	1) Проверка правильности выполнения заданий 2) Оценка результатов выполнения заданий	Ответы на поставленные вопросы, пояснения полученных результатов.

Основные понятия.

Расстояние от точки до плоскости – длина перпендикуляра, опущенного из точки на эту плоскость.

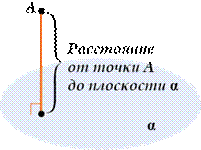
Существует, по крайней мере, два способа найти расстояние от точки до плоскости: геометрический и алгебраический.

При геометрическом способе нужно сначала понять, как расположен перпендикуляр из точки на плоскость: может он лежит в какой–то удобной плоскости, является высотой в какой-нибудь удобном (или не очень) треугольнике, а может этот перпендикуляр вообще является высотой в какой-нибудь пирамиде.

После этого первого и самого сложного этапа задача распадается на несколько конкретных планиметрических задач (быть может, в разных плоскостях).

При алгебраическом способе для того, чтобы найти расстояние от точки до плоскости, нужно ввести систему координат, найти координаты точки и уравнение плоскости, и после этого применить формулу расстояния от точки до плоскости.

Определение.

Расстояние от точки до плоскости – это длина перпендикуляра, опущенного из заданной точки к заданной плоскости.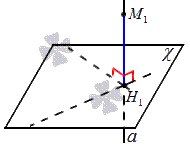

Перпендикуляр, опущенный из заданной точки на заданную плоскость, всегда меньше наклонной, проведенной из этой же точки к заданной плоскости.

Для решения различных задач можно использовать наиболее подходящий метод. Решив задачу одним методом, другим методом можно проверить правильность полученного результата.

Определение. Расстояние от точки до плоскости, не содержащей эту точку, есть длина отрезка перпендикуляра, опущенного из этой точки на данную плоскость.

Задача. Дан прямоугольный параллелепипед АBСDA ₁ B ₁ C ₁ D ₁ со сторонами AB =2, BC =4, AA ₁=6. Найдите расстояние от точки D до плоскости АСD ₁.

Используя определение. Найти расстояние r(D, АСD ₁) от точки D до плоскости АСD ₁ (рис. 1).

 

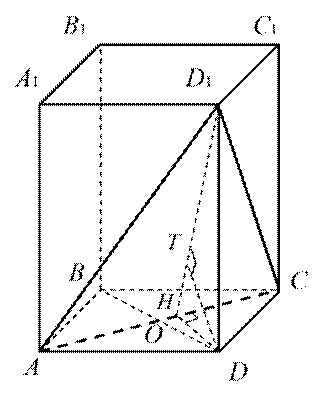
Рисунок 1.

Проведем DH ⊥ АС, следовательно, по тереме о трех перпендикулярах D ₁ H ⊥ АС и(DD ₁ H)⊥ АС. Проведемпрямую DT перпендикулярно D ₁ H. Прямая DT лежит в плоскости DD ₁ H, следовательно DT ⊥ AC. Следовательно, DT ⊥ АСD _1.

Из прямоугольного треугольника АDC найдем гипотенузу АС и высоту DH

 

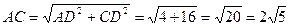
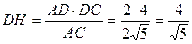
Из прямоугольного треугольника D ₁ DH найдем гипотенузу D ₁ H и высоту DT

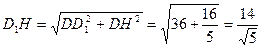
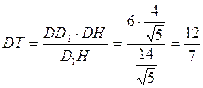
Ответ: .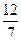

 

 

Координатный метод.

Пусть дана точка M (x ₀, y ₀, z ₀) и плоскость α, заданная уравнением ax + by + cz + d =0 в прямоугольной декартовой системе координат. Расстояние от точки M до плоскости α можно вычислить по формуле:

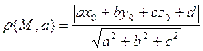
Введем систему координат (рис. 3). Начало координат в точке В;

прямая АВ — ось х, прямая ВС — ось y, прямая BB ₁ — ось z.

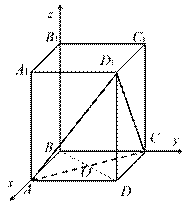Рисунок 3.

B (0,0,0), А (2,0,0), С (0,4,0), D (2,4,0), D ₁(2,4,6).

Пусть aх+by+cz+d =0 –  уравнение плоскости ACD ₁. Подставляя в него координаты точек A, C, D ₁ получим: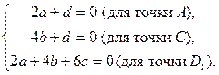

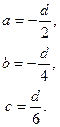
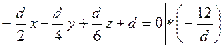
Уравнение плоскости ACD ₁ примет вид

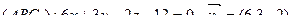
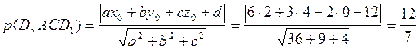
Ответ: .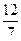

Общим перпендикуляром двух скрещивающихся прямых называется отрезок с концами на этих прямых, являющийся перпендикуляром к каждой из них.

Расстоянием между скрещивающимися прямыми называется длина их общего перпендикуляра. Оно равно расстоянию между параллельными плоскостями, проходящими через эти прямые. Для того чтобы найти расстояние между скрещивающимися прямыми, необходимо построить их общий перпендикуляр.

Семь способов нахождения расстояния между скрещивающимися прямыми:

1. Построить общий перпендикуляр двух скрещивающихся прямых (отрезок с концами на этих прямых и перпендикулярный обеим) и найти его длину.
2. Построить плоскость, содержащую одну из прямых и параллельную второй. Тогда искомое расстояние будет равно расстоянию от какой нибудь точки второй прямой до построенной плоскости.
3. Заключить данные прямые в параллельные плоскости, проходящие через данные скрещивающиеся прямые, и найти расстояние между этими плоскостями.
4. Построить плоскость, перпендикулярную одной из данных прямых, и построить на этой плоскости ортогональную проекцию второй прямой.
5. Вычисляется по формуле d = 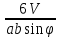где a и b данные скрещивающиеся прямые, являющиеся скрещивающимися рёбрами треугольной пирамиды, а 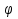– угол между этими прямыми.
6. Определяется с помощью векторного метода.

Задачу сводим к определению длины вектора, принадлежащего перпендикуляру, являющемуся общим перпендикуляром двух скрещивающихся прямых;

Определяется с помощью координатно-векторного метода.

·
Находим координаты концов отрезка, являющегося общим перпендикуляром двух скрещивающихся прямых;

·
Находим расстояние между двумя точками.

Рассмотрим применение данного способа при решении конкретных задач, для этого выделим алгоритм применения метода проекций:

1. 
   Выбираем плоскость, перпендикулярную одной из скрещивающихся прямых;
2. 
   Проецируем каждую прямую на эту плоскость;
3. 
   Расстояние между проекциями будет расстоянием между скрещивающимися прямыми.

Задача 1.
В единичном кубе найти расстояние между ребром и диагональю, не пересекающей его грани.

Решение.

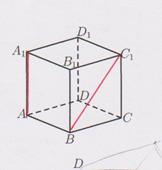
Пусть данное ребро АА₁ и диагональ BC₁. Плоскость АBC перпендикулярна прямой АА₁. Точка А — проекция АА₁ на эту плоскость. Проекция B C ₁ на плоскость (АBC) является прямая BC. Расстояние от точки А до прямой BC равно АВ = 1.

Ответ.1.

Задача 2.
В правильной треугольной призме ABC 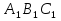, все ребра которой равны 1, найдите расстояние между прямыми AA ₁ и BC ₁.

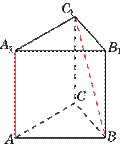
Решение:
Плоскость (АBC) перпендикулярна прямой АА₁. Точка А — проекция АА₁ на эту плоскость. Проекцией B C ₁ на плоскость (АBC) является прямая BC. Расстояние от точки А до прямой BC равно высоте треугольника АВС проведённой к стороне ВС. Площадь равностороннего треугольника вычисляется по формуле S = 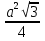= 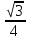. H = 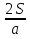h = = h = .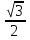
Ответ. .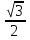
Задача 3.
В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁, все ребра которой равны 1, найдите расстояние между прямыми АА₁ и BC ₁.

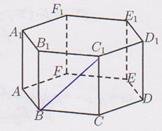
Решение.
Плоскость (АВС) перпендикулярна прямой АА₁. Точка ^ А — проекция АА₁ на эту плоскость. Проекцией B C ₁ на плоскость АBC является прямая BC. Расстояние от точки А до прямой BC равно длине перпендикуляра, опущенного из точки А на прямую ВС, оно является высотой треугольника АВС, проведённой к стороне ВС. Высоту треугольника вычислим по формуле h = 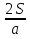, где S – площадь данного треугольника, а – длина стороны ВС. В АВС: АВ =1, ВС = 1(по условию), АС = √3 (по теореме косинусов). S = 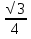(по формуле Герона), h = 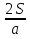= (2∙ = .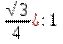

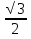Ответ. .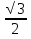
Задача 4.
Дана правильная пирамида PABC c боковым ребром РА равным 3 и стороной основания 2. Найдите расстояние между прямыми AВ и РC.
Решение:

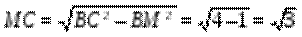Плоскость РМС перпендикулярна прямой АВ. Проекция прямой АВ на плоскость РМС – точка М. проекция прямой РО – сама прямая, так как она лежит в этой плоскости. Искомое расстояние – длина перпендикуляра от точки М до прямой РС, то есть высота треугольника МРС, проведённая к стороне РС, которая находится по формуле h = 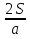. В МРС: РС =3,

 

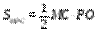
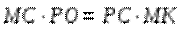
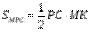
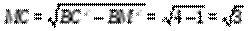
Практические задания:

Решите следующие задачи алгебраическим, координатным методом:

Вариант 1	Вариант 2
В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите расстояние от точки А до плоскости ВСА1.	В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите расстояние от точки А до плоскости СА1В1.
В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найдите расстояние от точки А до плоскости SCD	2. В правильной шестиугольной пирамиде SABCDEF, стороны основания которой равны 1, а боковые ребра равны 2, найдите расстояние от точки А до плоскости SDЕ.