Распространение световых волн в изотропных средах 1 страница

Теоретический материал

Дисперсия оптического излучения. Груповая скорость. Элементарная теория дисперсии: физическая модель вещества; силы, действующие на электрон в атоме; уравнение движения связанного электрона в поле плоской электромагнитной волны и его решение; выражение для показателя преломления в рамках классической теории дисперсии. Нормальная и аномальная дисперсия. дисперсионная кривая и ее приближенное описание.

Распространение света в проводящих средах. Комплексные диэлектрическая проницаемость и показатель преломления. Закон Бугера.

Законы отражения и преломления света на границе между диэлектриками. Разложение плоской волны на две со взаимно перпендикулярными линейными поляризациями. Формулы Френеля. Амплитудные и энергетические коэффициенты отражения и пропускания. Явление Брюстера. Соотношения между фазами волн при отражении и преломлении. Полное внутреннее отражение. Глубина проникновения света в оптически менее плотную среду. Преломление и отражение света на поверхности проводящей среды.

Основные типы задач

1. Рассматривая световой импульс, представляющий собой суперпозицию двух монохроматических волн и , найти групповую скорость этого импульса при условии . Под групповой скоростью волнового импульса понимают скорость перемещения максимума амплитуды рассматриваемого пакета.

Решение:

Найдем суммарную волну:

Пусть и – малые величины, тогда и и после подстановки в выражение для суммарной волны E получаем:

Это выражение описывает гармоническое колебание, характеризуемое частотой и волновым числом , с медленно меняющейся во времени и пространстве амплитудой

Амплитуда достигает максимального значения при

, (3.1)

где

Дифференцируя (3.1) получаем выражение для групповой скорости

Так как , то получаем:

2. В среде, состоящей из неполярных молекул (дипольный момент таких молекул в отсутствие внешнего поля равен нулю), распространяется плоская электромагнитная волна частоты . Рассматривая взаимодействие волны со связанными электронами, найти зависимость показателя преломления среды от частоты электромагнитной волны.

Решение:

На связанный электрон действует квазиупругая возвращающая сила , где – радиус-вектор смещения электрона от положения равновесия. В процессе колебаний электрон излучает электромагнитные волны, которые уносят энергию. Энергетические потери можно учесть, если ввести в рассмотрение тормозящую силу, действующую на электрон:

где – эффективный "коэффициент трения".

В поле внешней электромагнитной волны на электрон действует сила Лоренца , где – заряд электрона. При сила Лоренца становится равной: .

В результате уравнение движения электрона в поле внешней электромагнитной волны принимает вид:

где – масса электрона.

Для плоской электромагнитной волны уравнение движения перепишем в виде:

, (3.2)

где – собственная частота колебаний электрона в атоме (молекуле); –коэффициент затухания.

Решение дифференциального уравнения (3.2) будем искать в следующем виде:

Подставив это выражение в (3.2), получим:

где N – число молекул в единице объема; – вектор поляризации; , где – диэлектрическая восприимчивость среды.

Для диэлектрической проницаемости можно написать следующее выражение:

Так как , то

(3.3)

Оценки показывают, что второе слагаемое в (3.3) является малой величиной по сравнению с единицей. В этом случае (3.3) можно записать в виде:

(3.4)

Полученный показатель преломления является комплексной величиной, так как выражение (3.4) можно представить в виде: æ. Следовательно, действительная часть показателя преломления среды равна:

3. На границу раздела двух бесконечных диэлектриков с показателями преломления и под углом падает свет в виде плоской монохроматической волны. Исходя из условия одновременного существования на границе раздела падающей, отраженной и преломленной волн, получить законы отражения и преломления света.

Рис 3.1.

Решение:

Вектор напряженности электрического поля в электромагнитной волне в каждый момент времени можно разложить на две составляющие, ориентированные параллельно и перпендикулярно плоскости падения (рис. 3.1). Уравнение падающей плоской монохроматической волны, распространяющейся вдоль вектора имеет вид:

где А – амплитуда; – круговая частота; – радиус-вектор точки пространства в системе координат .

Если система координат выбрана так, что плоскость падения лежит в плоскости (рис 3.1), то и .

Так как , , , то

где – скорость распространения света в первой среде.

Аналогично для отраженного и преломленного света имеем:

где – скорость распространения света во второй среде, и - амплитуды отраженной и прошедшей волн соответственно.

На границе раздела сред () можно написать следующее:

На этой границе отраженная волна и преломленная волна должны изменяться так же, как и падающая волна E. Другими словами, фазы всех трех волн должны совпадать, т.е.

Из последнего равенства следует:

где – относительный показатель преломления.

Последние два выражения вместе с дополнительным утверждением, что отраженный и преломленный лучи лежат в плоскости падения, представляют собой законы отражения и преломления света.

4. На основании условия предыдущей задачи найти связь между амплитудами падающей, отраженной и преломленной волн (формулы Френеля).

Решение:

Граничные условия для нормальных , и тангенциальных , составляющих напряженностей электрического и магнитного полей на границе раздела двух сред имеют вид:

; ; ; , (3.5)

где учтено, что для большинства рассматриваемых сред .

Пусть падающая волна поляризована в плоскости падения. В этом случае нормальная составляющая магнитного поля отсутствует, и граничные условия (3.5) запишутся в виде:

(3.6)

При записи последнего равенства была использована связь между абсолютными значениями векторов и в плоской электромагнитной волне:

Используя законы отражения и преломления (см. предыдущую задачу) и тригонометрические равенства:

из граничных условий (3.6) находим:

(3.7)

Аналогично для перпендикулярных компонент рассматриваемых амплитуд можно получить:

(3.8)

Формулы (3.7) и (3.8) называются формулами Френеля.

5. Плоская монохроматическая волна распространяется из оптически более плотной среды в менее плотную так, что на границе раздела происходит полное внутреннее отражение. Относительный показатель преломления . Определите характер световой волны в оптически менее плотной среде.

Рис 3.2.

Решение:

Если полного внутреннего отражения не происходит, то световая волна во второй среде имеет вид (рис. 3.2):

где угол преломления связан с углом падения следующим законом:

При полном внутреннем отражении и существует диапазон углов падения , при котором оказывается большим 1.

Запишем формально:

(3.9)

Запишем выражение для преломленной волны в экспоненциальной форме:

(3.10)

Подставив (3.9) в (3.10), получим:

Знак "+" в первой exp не имеет физического смысла. Окончательно получаем:

Это выражение описывает неоднородную волну, распространяющуюся вдоль поверхности раздела сред в направлении оси . Амплитуда волны быстро убывает с увеличением координаты 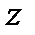. Эффективная глубина проникновения для скользящего луча соизмерима с величиной порядка , т.е. порядка длины волны.

6. Доказать, что в случае полного внутреннего отражения интенсивность отраженного и падающего света равны.

Решение:

Преобразуем формулы Френеля:

Подставляя в записанные формулы Френеля выражение

Получаем

(3.11)

Числители и знаменатели в правой части каждой из формул (3.11) являются комплексно сопряженными числами, откуда следует, что , .

Другими словами, для каждой компоненты интенсивность света, отраженного при полном внутреннем отражении, равна интенсивности соответствующей компоненты падающего света, т.е. , Окончательно получаем:

Задачи для самостоятельного решения.

1. Выразить групповую скорость через фазовую скорость и , а так же через и .

Ответ: ; .

2. Найти относительное отклонение групповой скорости от фазовой в среде с показателем преломления , для которой при .

Ответ: .

3. Вычислить групповую скорость для различных законов дисперсии, если фазовая скорость равна:

1) – недиспергирующая среда;

2) – волны на поверхности воды, вызываемые силой тяжести;

3) – капиллярные волны;

4) – поперечные колебания стержня;

5) – электромагнитные волны в ионосфере ( – скорость света в вакууме).

Ответ: 1) ; 2) ; 3) ; 4) ; 5) .

4. Показать, что касательная в точке А с абсциссой к кривой ( – фазовая скорость) отсекает на оси ординат отрезок, равный групповой скорости для (рис. 3.3).

Рис 3.3.

5. При каком законе изменения диэлектрической проницаемости немагнитной среды, заполняющей бесконечное пространство, связь между фазовой и групповой скоростями электромагнитных волн принимает вид

Ответ: , где .

6. Пусть электромагнитное излучение распространяется в немагнитной среде с дисперсией . В соответствии с теорией относительности сигнал не может распространяться со скоростью, большей, чем . Какое ограничение накладывает это условие на возможную зависимость ?

Ответ: .

7. В результате измерения показателя преломления сероуглерода получено, что при ; при ; при Найти соотношение между фазовой и групповой скоростями.

Указание: Воспользоваться ответом к задаче 1.

8. Предположим, что в стекле дисперсия определяется резонансной частотой . Какой вид имеет закон дисперсии в этом случае, если затуханием пренебречь?

Ответ: , где ; – число резонирующих электронов в единице объема.

9. На основании условия предыдущей задачи вычислить групповую скорость света.

Ответ: , где – скорость света в вакууме.

10. Высокочастотная электромагнитная волна (например, рентгеновское излучение) распространяется в среде, характеризуемой числом молекул в единице объема N. Найти зависимость показателя преломления среды от частоты рассматриваемой волны.

Указание: Воспользоваться формулой (3.5) при .

11. Вывести закон поглощения (закон Бугера) для плоской волны, распространяющейся вдоль оси , исходя из предположения, что в слое толщиной поглощается определенная часть падающего света, т.е. что показатель поглощения не зависит от интенсивности света.

Ответ: .

12. Получить формулы Френеля для нормального падения света на границу раздела вакуума и прозрачного диэлектрика с показателем преломления .

Указание: Направления векторов в падающей, отраженной и преломленной волнах взять в соответствии с рис. 3.1.

Ответ:

13. Найти интенсивность отраженной и преломленной волн на границе двух сред с показателями преломления и , соответственно, если интенсивность падающего света .