2020-05-12
563
,
где 
, 
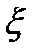– координаты в плоскости отверстия; 
, 
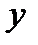– координаты в плоскости наблюдения; 
– площадь отверстия.
Для любой точки на оси 
, и поэтому,
.
Перейдем к полярным координатам:
; 
;
Перейдя к интенсивности, получим:
,
причем 
, где 
– интенсивность света в точке Qпри отсутствии экрана с отверстием; 
при 
или 
, где 
– целое число, т.е. когда на отверстии укладывается четное число зон Френеля. При 
интенсивность света монотонно уменьшается до нуля.
При малом числе зон Френеля, открываемых отверстием, справедливо 
. Считая допустимое отклонение 
от единицы не более 10%, оценим расстояние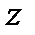 
:
.
Откуда получаем:
или 
Следовательно, расстояние до экрана от диафрагмы с отверстием должно удовлетворять условию 
На отверстии при этом укладывается следующее число зон Френеля:
.
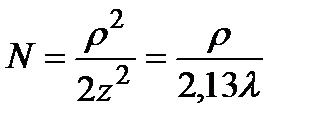Например, при 
и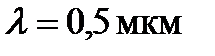 
количество открытых зон Френеля 
.
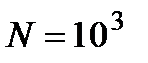2. Рассчитать параметры (общее число 
зон Френеля и радиус 
каждой зоны) амплитудной зонной пластинки, обеспечивающей изображение точечного истоникка А в точке В (рис. 5.4.). Положение точек А и В заданы отрезками 
и 
, радиус зонной пластинки (отверстия) -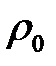 
, длина волны - 
.
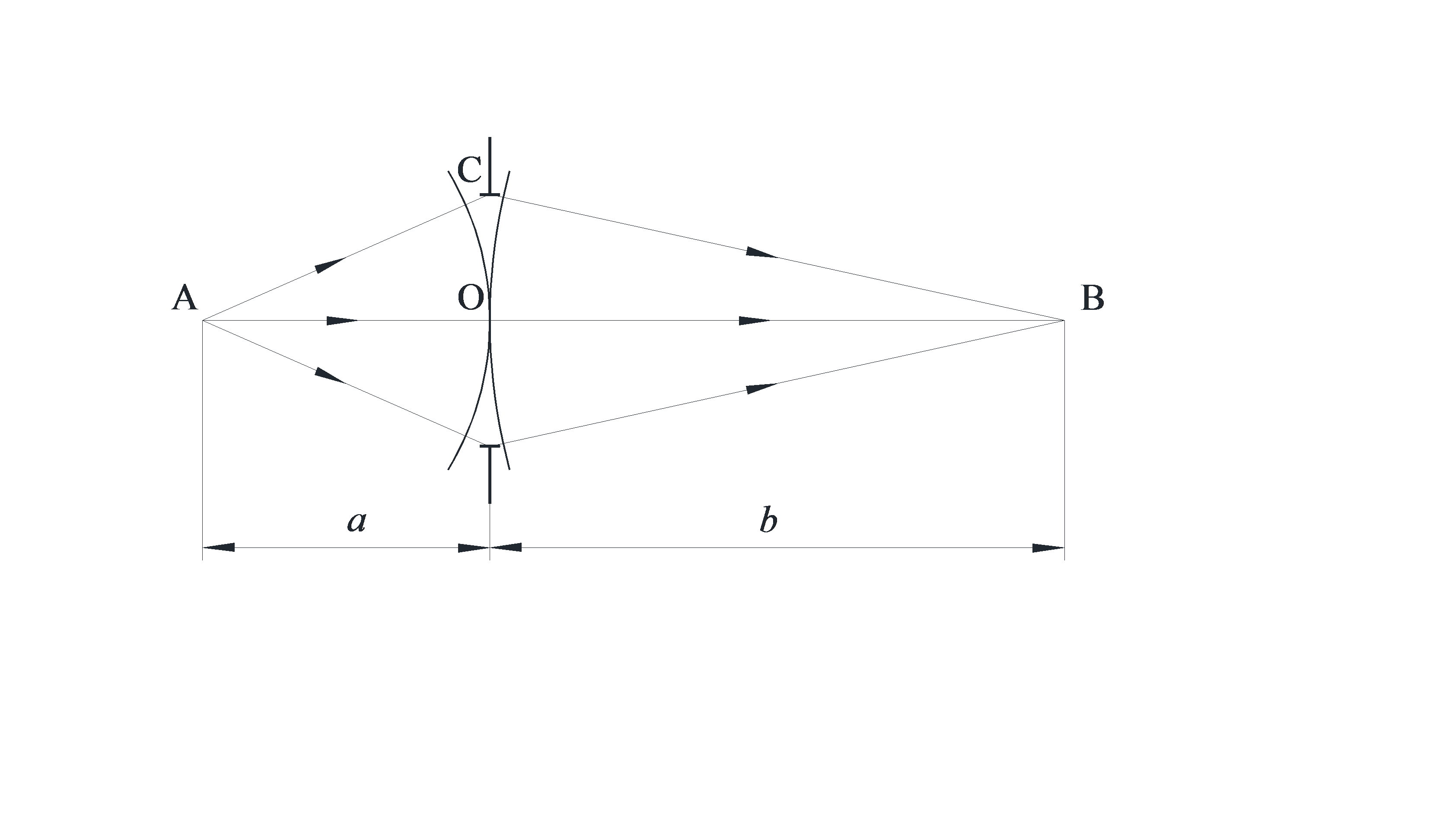
Рис. 5.4.
Решение. Пусть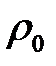 
– радиус последней m- ой зоны. Оптическая разность хода лучей, идущих в точку В через край m- ой зоны (ABC) и вдоль оптической оси (AOB), равна:
Кроме того, по определению зонной пластинки имеем:
.
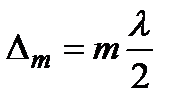Тогда получаем следующее выражение:
Введем понятие фокусного расстояния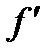 
пластинки:
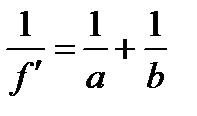
Тогда общее число зон будет равно
.
Аналогично для радиуса 
ой зоны 
получаем:
.
4. Тонкая линза с фокусным расстоянием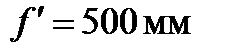 
фокусирует параллельный пучок монохроматического излучения (
). Диаметр линзы 
. Во сколько раз интенсивность света в фокусе линзы превышает интенсивность падающего излучения.
Решение:
Применим дифракционный интеграл Френеля-Кирхгофа в приближении Френеля:
где 
- амплитуда падающей волны,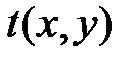 
– амплитудный коэффициент пропускания линзы; 
– координаты в плоскости линзы.
В параксиальном приближении для тонкой линзы, работающей, как фазовый транспарант:
.
Для заднего фокуса 
линзы имеем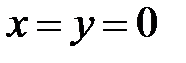 
и,следовательно:
,
поэтому интенсивность света в фокусе линзы
,
то есть примерно в миллион раз выще интенсивности падающей волны.
4. Найти распределение интенсивности в дифракционной картине Фраунгофера при нормальном освещении амплитудной дифракционной решетки с периодом 
и шириной щелей 
(рис. 5.5).
Рис 5.5.
Решение:
В направлении угла 
элементарный участок m -ой щели посылает волну:
,
где 
– координата, отсчитываемая от края m -ой щели.
Вся m -ая щель посылает волну:
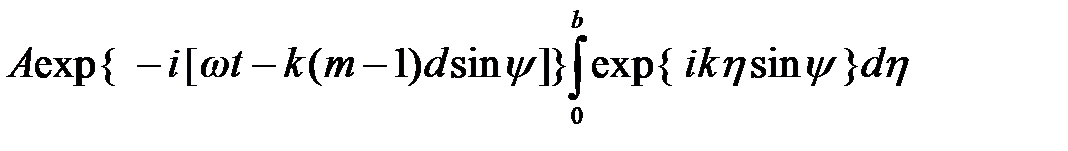
От всех N щелей, являющихся когерентными излучателями, получим следующее выражение для комплексной амплитуды волны в направлении угла 
:
(5.1)
Вычислим выходящий в выражение (5.1) интеграл:
.
Воспользовавшись формой Эйлера, получаем:
,
где 
.
Вычислим входящую в выражение (5.1) сумму, используя формулу для геометрической прогрессии и введя обозначение 
:
.
В результате выражение (5.1) можно переписать в следующем виде:
(5.2)
Переходя к интенсивности света, получаем:
(5.3)
где , ,
– распределение интенсивность в дифракционной картине, создаваемой только одним периодом дифракционной решетки.
Максимумы интенсивности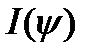 
определяются условием:
, где 
, 
, 
,… (5.4)
они называются главными максимумами.
5. Показать, что для дифракционной решетки с периодом 
(
– ширина щели), все четные главные максимумы обращаются в 0.
Решение:
Значение интенсивности в главных максимумах можно определить из выражения (5.3) при подстановке в него условия (5.4):
,
которое с учетом соотношения принимает вид:
Анализ этого выражения показывает, что при четном порядке главного максимума значение интенсивности обращается в 0, а при нечетном:
.
6. Прозрачная периодическая структура, профиль которой изображен на рис. 5.6, освещается нормально падающей плоской монохроматической волной. При заданном показателе преломления п подобрать высоту ступени h, чтобы главный максимум первого порядка был максимально интенсивен. Чему равна в этом случае интенсивность максимума нулевого порядка?
Рис 5.6.
Решение:
Воспользуемся результатом решения задачи 4. Согласно формуле (5.3) результат дифракции на периодической структуре определяется дифракцией на одном периоде такой структуры 
и интерференцией волн от всех периодов, учитываемых отношением 
.
Найдем распределение интенсивность в дифракционной картине, создаваемой только одним периодом периодической структуры, состоящим из участков I и II (рис 5.6).
Пусть 
– комплексная амплитуда волны, дифрагировавшей на участке I. В силу того, что 
, линейный размер участка Iравен линейному размеру участка II, а следовательно модуль комплексной амплитуды волны от участка Iравен модулю комплексной амплитуды волны от участка II. Однако, волна от участкаII оказывается сдвинута по фазе на некоторую величину 
:
При суммировании волн получаем:
.
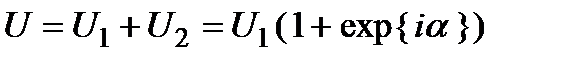Переходя к интенсивности суммарного поля, подучаем:
, (5.5)
где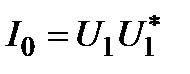 
.
Для того, чтобы интенсивность в главном максимуме первого порядка была максимальна из выражения (5.5) следует, что должно выполнить условие:
. (5.6)
Для вычисления 
найдем оптическую разность хода 
между лучами 1 и 2 в зависимость от угла дифракции 
(рис. 5.7):
.
Соответствующая разность фаз равна:
Рис. 5.7.
Подставляя выражение для 
в выражение (5.6), получим значение высоты профиля:
.
При этом для главного максимума нулевого порядка 
и, следовательно, из выражения (5.5) получаем, что 
. А так как , то интенсивность всех главных максимумов четных порядков также становится равной нулю.
Задачи для самостоятельного решения
1. Квадратное отверстие освещается параллельным пучком солнечных лучей в спектральном диапазоне (
), падающих нормально к плоскости отверстия. Длина стороны квадратного отверстия 
. Найти размер 
дифракционной картины на экране, удаленном на 
от отверстия. Границей освещенности на экране считать положение первого дифракционного минимума наиболее сильно отклоненных лучей.
Ответ: 
.
2. Параллельный пучок монохроматического света (
) падает нормально на щель шириной 
. Объектив с фокусным расстоянием 
расположен за щелью. Какова линейная ширина центрального дифракционного максимума, наблюдаемого в фокальной плоскости объектива?
Ответ: 
.
3. Параллельный пучок монохроматического света падает на проволоку диаметром 
, натянутую перпендикулярно к направлению распространения света. На экране, расположенном перпендикулярно к направлению распространения света, на расстоянии 
от проволоки наблюдаются дифракционные полосы, расстояние между которыми . Найти длину волны света.
Ответ: 
.
4. Параллельный пучок монохроматического света диаметром 
, расходимость которого определяется только дифракцией, направлен на Луну. Определить диаметр освещенного на Луне участка поверхности, если 
, а расстояние от Земли до Луны 
. Расстоянием в атмосфере пренебречь.
Ответ: 
.
5. Точечный источник монохроматического света расположен на расстоянии 
от круглого отверстия, а экран – с противоположной стороны на расстоянии 
. При каких значениях радиуса 
отверстия центр наблюдаемых на экране дифракционных колец будет светлым и при каких – темным? Вычислить диаметры отверстий 
, 
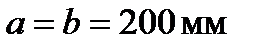, соответствующих первой и второй зонам Френеля, при 
и .
Ответ: при 
– центр картины светлый; при 
– темный,
где ;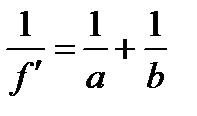
; 
6. На длиннофокусную тонкую собирающую линзу c ирисовой диафрагмой падает параллельный пучок монохроматического света. На расстоянии от линзы помещен экран, на котором наблюдаются дифракционные кольца. При каких радиусах диафрагмы центр колец будет светлым, а при каких - темным?
Ответ: 
, при 
;
, при 
.
где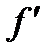 
– фокусное расстояние линзы. Центр колец будет темным если 
– четное число.
7. Плоскую пластину с радиусами колец, пропорциональным квадратному корню из целых чисел, приближенно можно считать зоной пластиной Френеля: при значительном увеличении числа зон Френеля наблюдается заметное ухудшение качества изображения. Рассчитать допустимое число N прозрачных зон, если точечный источник и точка наблюдения находятся соответственно на расстояниях 
и 
от пластины, а длина волны 
.
Указание: чтобы не вносить заметной ошибки в амплитуду, оптическая разность хода по сравнению с квадратичным приближением должна быть меньше 
.
Ответ: 
.
8. В камере с малым отверстием расстояние от отверстия до фотопластинки 
. Необходимо получить изображение Солнца в видимом спектре (
). Определить диаметр отверстия, чтобы изображение было наилучшим
Ответ: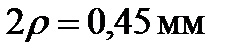 
.
9. Рассчитать распределение комплексной амплитуды дифрагирующей волны лазерного излучения при гауссовом распределении амплитуда на плоском волновом фронте (рис. 5.8):
.
Рис 5.8.
Указание. Воспользоваться интегралом Френеля-Кирхгофа:
,
где 
,
а также интегралом Пуассона:
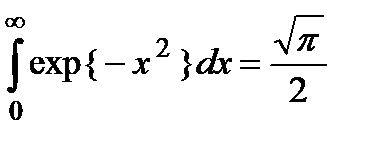
Ответ: 
,
где 
; 
; 
.
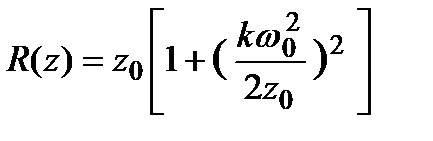10. Вычислить минимальное число штрихов решетки, которая может разрешить натриевый дублет в спектре первого порядка (
; 
).
Ответ: 
.
11. Плоская амплитудная дифракционная решетка с отношением ширины щели к периоду 
освещается нормально падающей плоской волной длиной 
. Найти отношение интенсивностей в максимумах первого и шестого порядков дифракции, полученных с помощью этой решетки.
Ответ: 
.
12. Найти распределение интенсивности 
в дифрагированной волне, если плоская монохроматическая волна падает по нормали на фазовую решетку с показателем преломления 
, профиль штрихов, которой показан на рис. 5.9. Определить число главных дифракционных максимумов, наблюдаемых в дифракционной картине.
Рис 5.9.
Ответ: 
где 
, ;
наблюдается один главный дифракционный максимум при 
.
13. Найти распределение интенсивности в дифрагированной волне при падении по нормали плоской монохроматической волны на амплитудную решетку, коэффициент пропускания которой изменяется по синусоидальному закону в направлении оси 
и постоянен в направлении оси 
. Известно, что амплитуда прошедшей волны сразу за решеткой зависит от координаты 
по закону: 
, где 
, 
- период решетки. Максимумы каких порядков наблюдаются на такой решетке?
Ответ: 
где ; 
- общее число периодов.
Наблюдаются три дифракционных максимума при 
.
14. Дифракционная решетка имее 
штрихов на 1 мм. Под каким углом должно падать на решетку излучение длиной волны 
, чтобы в направлении перпендикулярном к решетке, образовался дифракционный максимум второго порядка.
