Аналогичный вывод можно сделать и для волны распространяющейся со скоростью 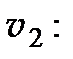 составляющие вектора
составляющие вектора 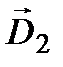 относятся следующим образом:
относятся следующим образом:
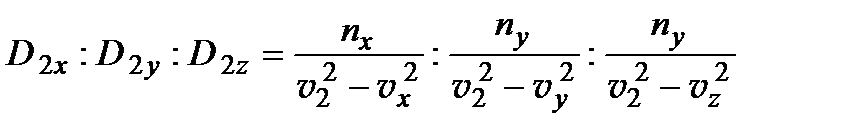 .
.
Теперь докажем, что плоскости колебаний векторов 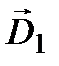 и
и 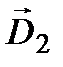 взаимно перпендикулярны. Для этого запишем выражение (6.1) для каждой из рассматриваемых волн:
взаимно перпендикулярны. Для этого запишем выражение (6.1) для каждой из рассматриваемых волн:
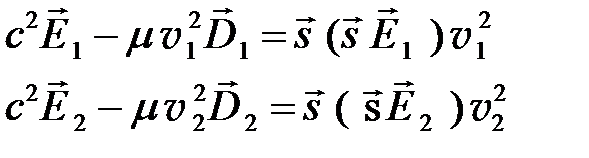 (6.12)
(6.12)
Умножим скалярно первое уравнение (6.12) на 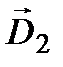 , а второе – на
, а второе – на 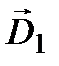 и вычтем из второго уравнения первое. Тогда с учетом того, что
и вычтем из второго уравнения первое. Тогда с учетом того, что 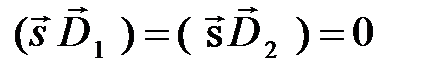 , получим:
, получим:
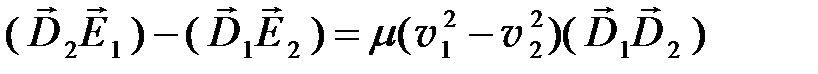 (6.13)
(6.13)
Раскрывая в левой части (6.10) скалярные произведения с учетом того, что
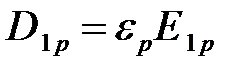 ,
, 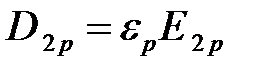
получаем:
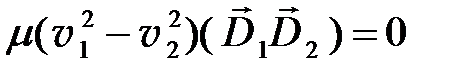
Следовательно, если 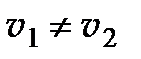 , то
, то 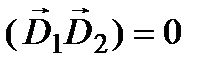 , т.е. плоскости колебаний векторов
, т.е. плоскости колебаний векторов 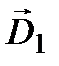 и
и 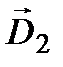 взаимно перпендикулярны.
взаимно перпендикулярны.
4. Прямая, вдоль которой фазовые скорости обеих линейно поляризованных волн, распространяющихся в кристалле, одинаковы, называется оптической осью первого рода. Показать, что в кристалле существуют две оптические оси, и, рассмотрев случай вырождения двухосной кристалла в одноосный, вычислить фазовые скорости распространения волны в этом случае.
Решение:
В случае если волна распространяется в анизотропной среде с фазовой скоростью 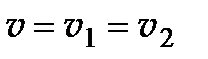 , то волновой вектор этой волны будет совпадать с оптической осью такой среды. Определив направление такого волнового вектора, получим направление оптической оси кристалла.
, то волновой вектор этой волны будет совпадать с оптической осью такой среды. Определив направление такого волнового вектора, получим направление оптической оси кристалла.
Из условия (6.11) следует, что равенство 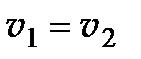 возможно, когда
возможно, когда 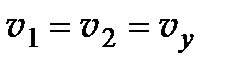 . В этом случае выражение (6.10) принимает вид:
. В этом случае выражение (6.10) принимает вид:
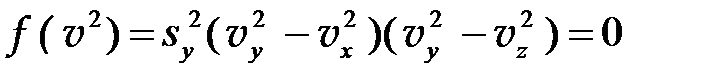 (6.14)
(6.14)
Если все три главные скорости 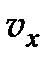 ,
, 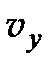 ,
, 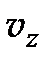 различны, то из (6.14) следует, что
различны, то из (6.14) следует, что 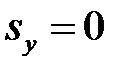 , т.е. волновой вектор лежит в плоскости
, т.е. волновой вектор лежит в плоскости 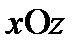 , а следовательно, оптические оси, если они существуют, также лежат в плоскости
, а следовательно, оптические оси, если они существуют, также лежат в плоскости 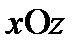 (рис. 6.3). Найдем угол между этим волновым вектором и осью
(рис. 6.3). Найдем угол между этим волновым вектором и осью 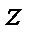 . Так как
. Так как 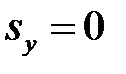 и
и 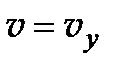 , то формула Френеля (6.6) принимает вид:
, то формула Френеля (6.6) принимает вид:
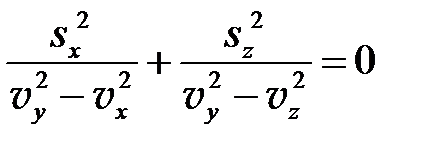 .
.
Откуда
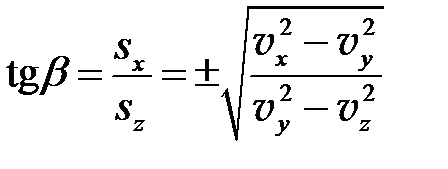 .
.
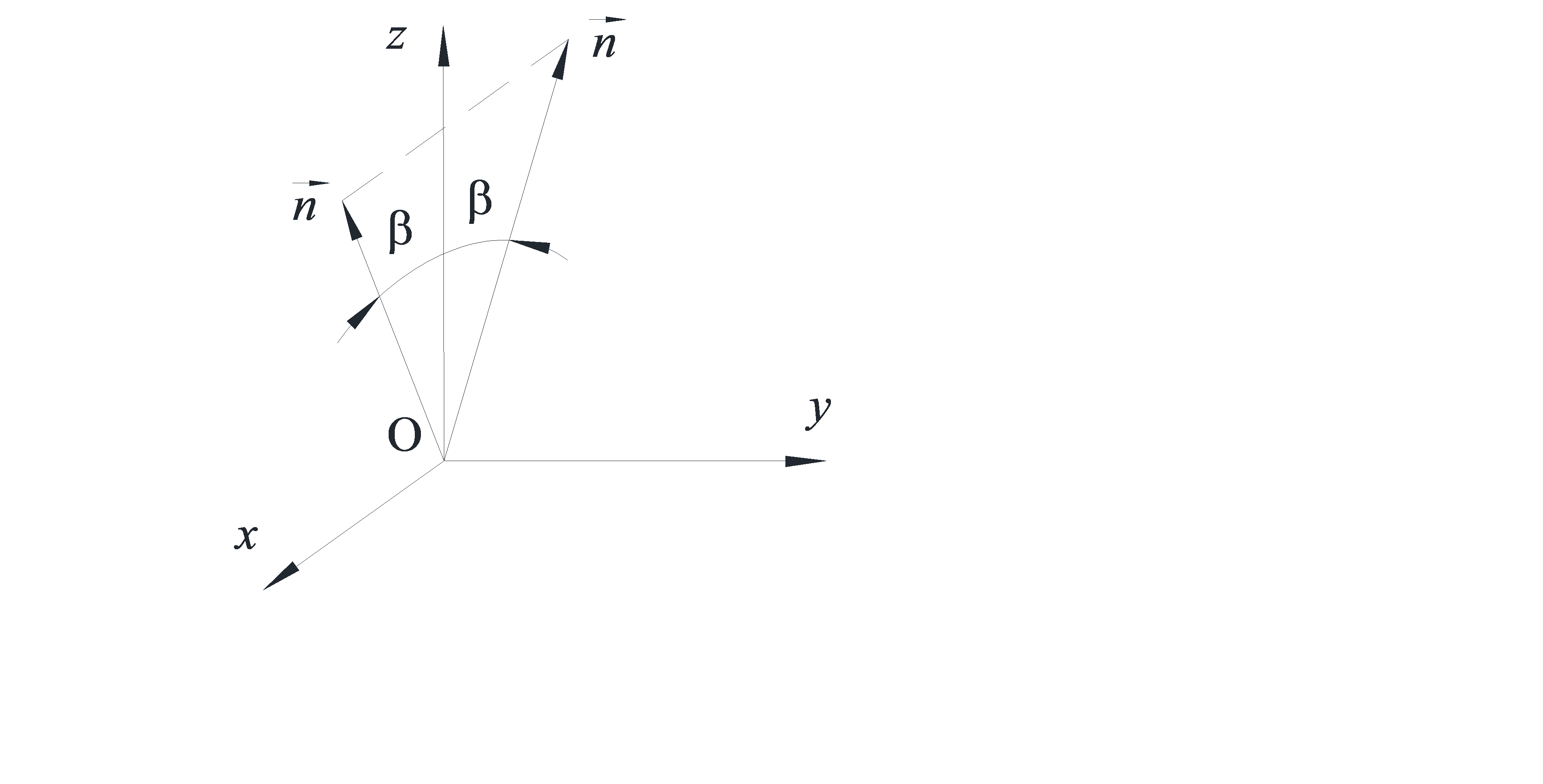
Рис 6.3.
Если ввести в рассмотрение главные показатели преломления кристалла:
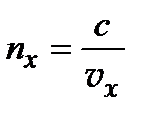 ,
, 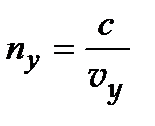 ,
, 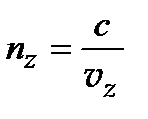 .
.
то
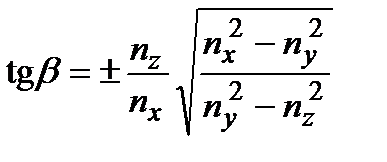 .
.
Таким образом, оптические оси лежат в плоскости 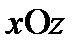 и расположены симметрично относительно оси
и расположены симметрично относительно оси 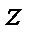 . Ясно, что оптически двухосный кристалл вырождается в одноосный, если оптическая ось совпадает либо с осью
. Ясно, что оптически двухосный кристалл вырождается в одноосный, если оптическая ось совпадает либо с осью 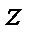 , либо с осью
, либо с осью 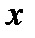 . Пусть оптическая ось совпадает с осью
. Пусть оптическая ось совпадает с осью 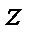 (положительный кристалл); в этом случае
(положительный кристалл); в этом случае 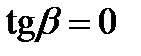 и, следовательно,
и, следовательно, 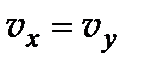 . Формула Френеля в этом случае принимает вид:
. Формула Френеля в этом случае принимает вид:
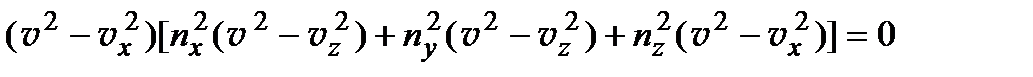 (6.12)
(6.12)
Первый корень этого уравнения 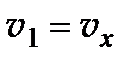 . Этому корню соответствует так называемая обыкновенная волна. Показатель преломления
. Этому корню соответствует так называемая обыкновенная волна. Показатель преломления 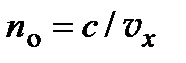 для этой волны не зависит от распространения.
для этой волны не зависит от распространения.
Второй корень уравнения (6.12)
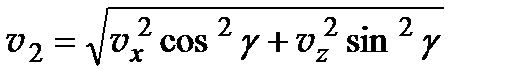 , (6.13)
, (6.13)
где 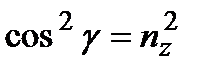 ,
, 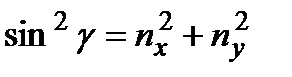 ,
, 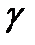 – угол между осью
– угол между осью 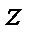 и нормированным вектором волновой нормали
и нормированным вектором волновой нормали 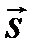 .
.
Формуле (6.13) соответствует необыкновенная волна. Показатель преломления необыкновенной волны 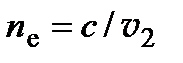 зависит от направления распространения волнового фронта. Как известно, вектор
зависит от направления распространения волнового фронта. Как известно, вектор 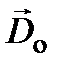 обыкновенной волны колеблется перпендикулярно к оптической оси, т.е. вдоль оси х, а вектор
обыкновенной волны колеблется перпендикулярно к оптической оси, т.е. вдоль оси х, а вектор 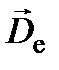 необыкновенной волны – вдоль оптической оси
необыкновенной волны – вдоль оптической оси 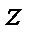 . Поскольку
. Поскольку 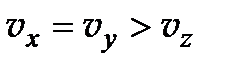 , скорость распространения обыкновенной волны больше скорости необыкновенной.
, скорость распространения обыкновенной волны больше скорости необыкновенной.
Направление, вдоль которого колеблется вектор 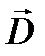 волны, распространяющейся с наибольшей скоростью в кристалле, называется быстрой осью, а наименьшей – медленной осью. В нашем примере быстрой осью является ось х.
волны, распространяющейся с наибольшей скоростью в кристалле, называется быстрой осью, а наименьшей – медленной осью. В нашем примере быстрой осью является ось х.
5. Призма Волластона изготовлена из исландского шпата так, что в левой части призмы оптическая ось параллельна плоскости чертежа (рис. 6.4), а в правой – перпендикулярна.
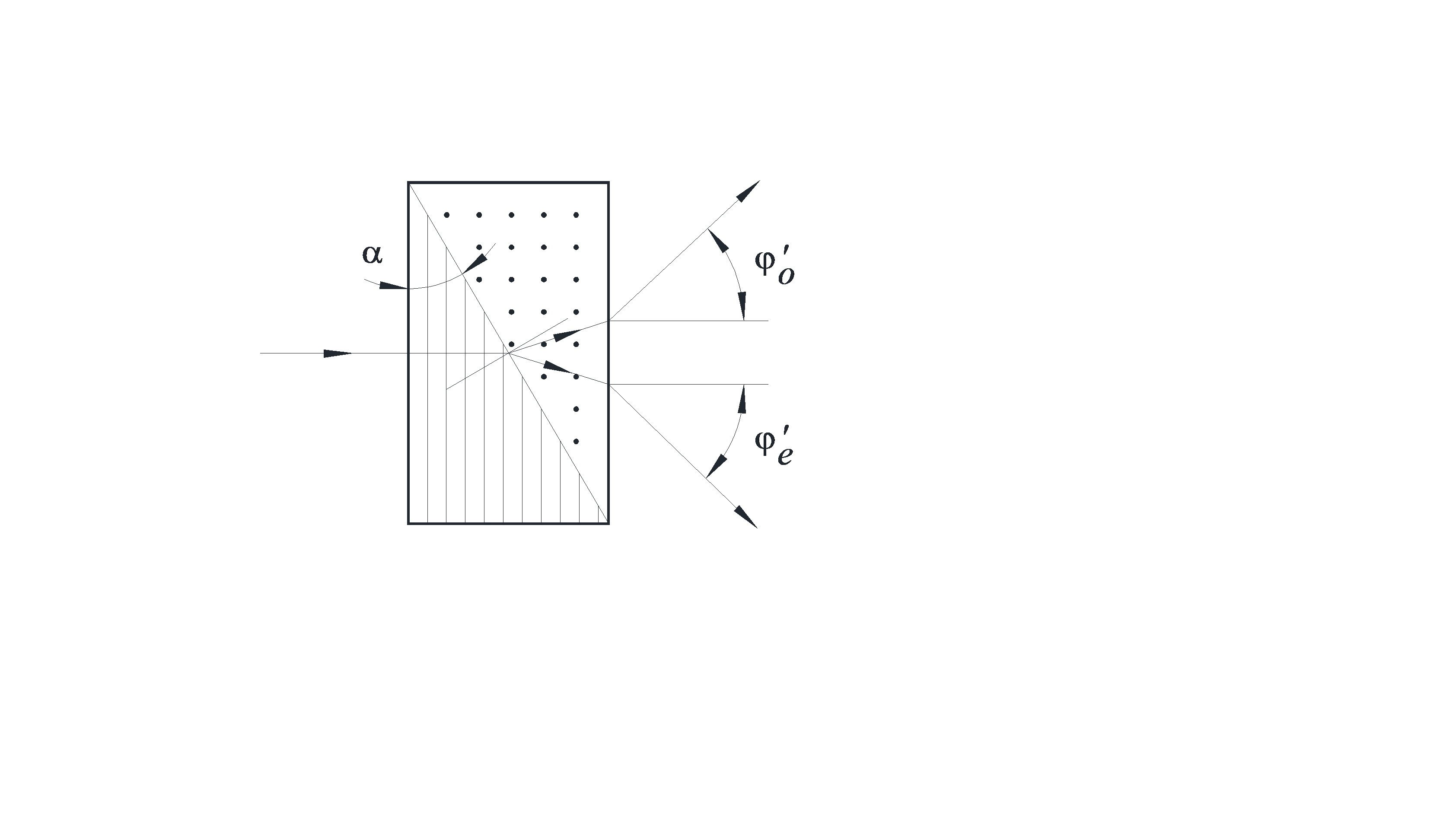
Рис. 6.4.
Показатель преломления обыкновенного луча 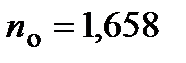
 необыкновенного
необыкновенного 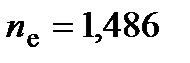
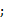 угол
угол 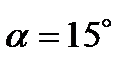 . Рассчитайте, на какой угол будут разведены обыкновенный и необыкновенный лучи.
. Рассчитайте, на какой угол будут разведены обыкновенный и необыкновенный лучи.
Решение:
В левой части призмы распространяются две волны - обыкновенная и необыкновенная, причем вектор 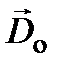 обыкновенной волны колеблется в плоскости, перпендикулярной к оптической оси, а вектор
обыкновенной волны колеблется в плоскости, перпендикулярной к оптической оси, а вектор 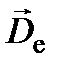 необыкновенной волны – параллельно оптической оси. После преломления на границе раздела сред обыкновенный луч становится необыкновенным и наоборот. Учитывая это, запишем закон преломления на границе раздела:
необыкновенной волны – параллельно оптической оси. После преломления на границе раздела сред обыкновенный луч становится необыкновенным и наоборот. Учитывая это, запишем закон преломления на границе раздела:
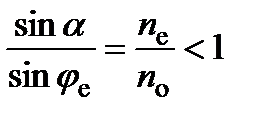 ;
; 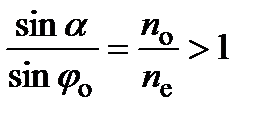 .
.
где 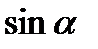 – синус угла падения на границу раздела сред в призме для обыкновенного и необыкновенного лучей, соответственно.
– синус угла падения на границу раздела сред в призме для обыкновенного и необыкновенного лучей, соответственно.
Законы преломления на границе раздела призма-воздух имеет вид:
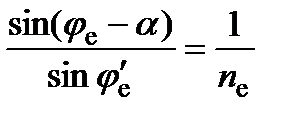 ;
; 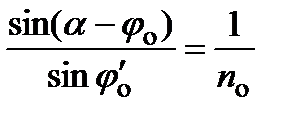 .
.
Подставляя численные значения из условия задачи, получаем:
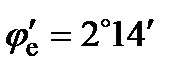 ;
; 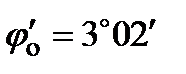 .
.
Следовательно, полный угол 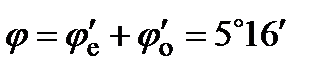 .
.
При решении многих задач в кристаллооптике полезно использовать матричное представление электромагнитных волн и преобразование этих полей при прохождении через кристаллы. В соответствии с этим представлением вектор 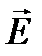 плоской электромагнитной волны, распространяющейся вдоль оси
плоской электромагнитной волны, распространяющейся вдоль оси 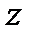 , описываемый выражением:
, описываемый выражением:
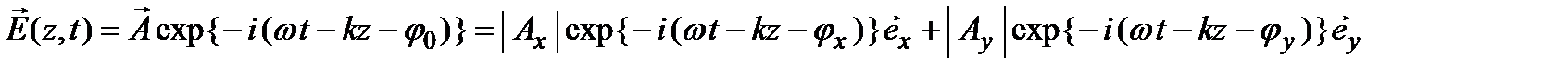 можно представить с помощью вектора Джонса:
можно представить с помощью вектора Джонса:
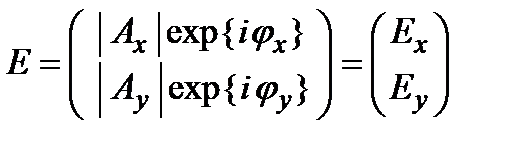 ,
,
где 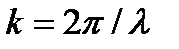 ;
; 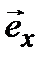 ,
, 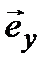 – единичные векторы, направленые вдоль положительных направлений осей
– единичные векторы, направленые вдоль положительных направлений осей 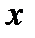 и
и 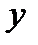 ;
; 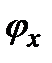 ,
, 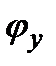 – начальные фазы составляющих колебаний.
– начальные фазы составляющих колебаний.
Восстановить полное описание электромагнитной волны можно, если вектор Джонса умножить на 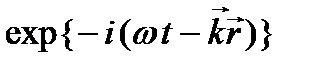 :
:
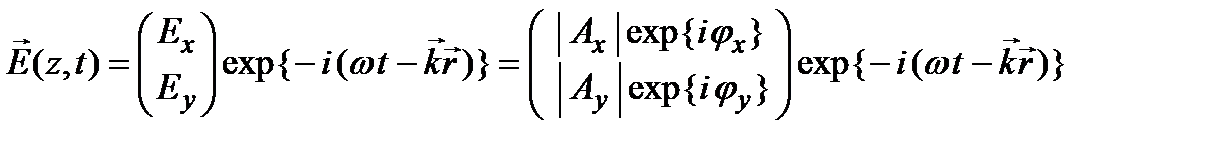
Обычно абсолютные значения фаз колебаний 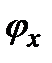 , и
, и 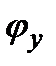 не представляют практического интереса, и более важным является значение разности фаз колебаний:
не представляют практического интереса, и более важным является значение разности фаз колебаний:
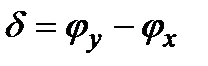 .
.
Поэтому векторы Джонса чаще записываются в виде:
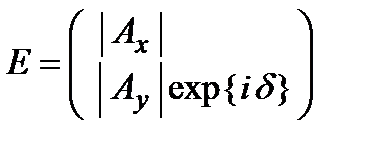
Интенсивность электромагнитной волны будем определять, умножая вектор Джонса 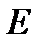 на эрмитово-сопряженный вектор
на эрмитово-сопряженный вектор 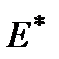 , т.е.:
, т.е.:
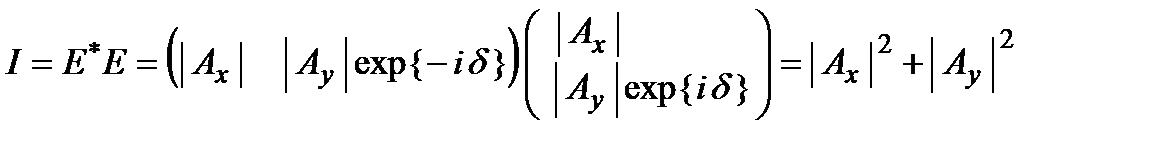
Обычно при расчетах полагают интенсивность волны равной 1, поэтому
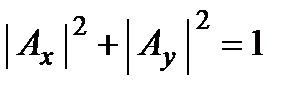 .
.
Основным достоинством введения вектора Джонса является то, что с его помощью легко описываются различные поляризационные состояния света. Так, для линейно поляризованного света единичной интенсивности с азимутом поляризации 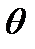 к оси
к оси 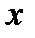 вектор Джонса имеет вид:
вектор Джонса имеет вид:
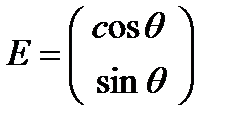 .
.
Для лево- и право- циркулярно-поляризованного света соответственно вектор Джонса имеет вид:
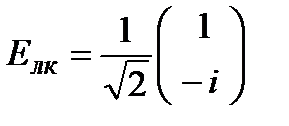 ;
; 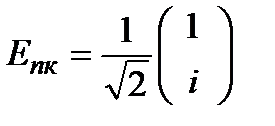
Для лево- и право- эллиптически поляризованного света с отношением малой или большой осей 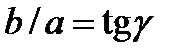 и с большой осью, направленной по оси
и с большой осью, направленной по оси 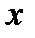 имеем:
имеем:
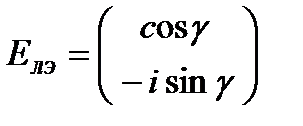
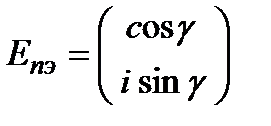 .
.
Чтобы получить вектор Джонса 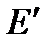 в системе координат
в системе координат 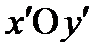 , повернутой на угол
, повернутой на угол 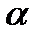 относительно системы х О у, необходимо воспользоваться матрицей поворота:
относительно системы х О у, необходимо воспользоваться матрицей поворота:
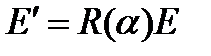
где 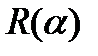 – матрица поворота:
– матрица поворота:
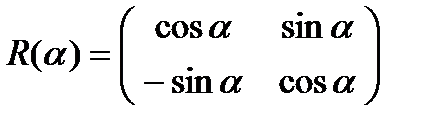
При прохождении излучения через элементы, изменяющие его состояние поляризации, вектор Джонса преобразуется следующим образом:
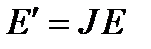 , (6.14)
, (6.14)
где 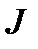 – матрица Джонса поляризационного элемента.
– матрица Джонса поляризационного элемента.
Ниже приведены матрицы Джонса для различных поляризационных элементов.
а. Идеальный линейный поляризатор, ориентированный под углом 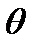 к оси
к оси 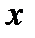 :
:
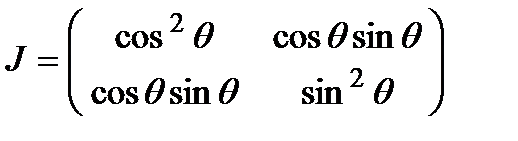
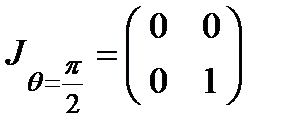 (6.15)
(6.15)
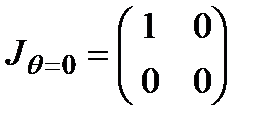
б. Фазовая пластинка, вносящая разностью фаз 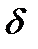 , быстрая ось которой ориентирована под углом
, быстрая ось которой ориентирована под углом 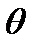 к оси
к оси 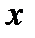 :
:
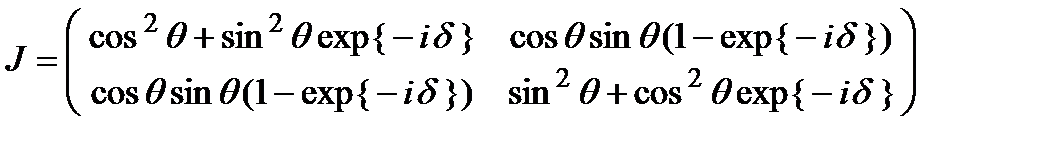
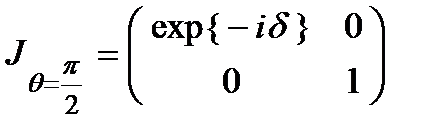 (6.16)
(6.16)
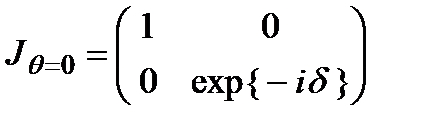
В том числе:
полуволновая пластинка (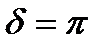 ):
):
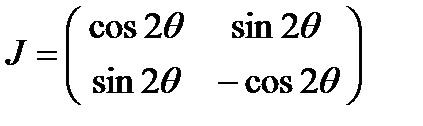
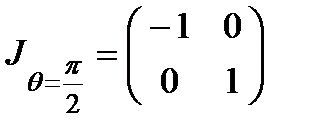
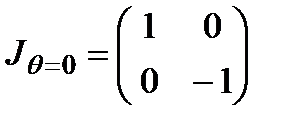
четвертьволновая пластинка (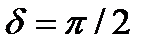 ):
):
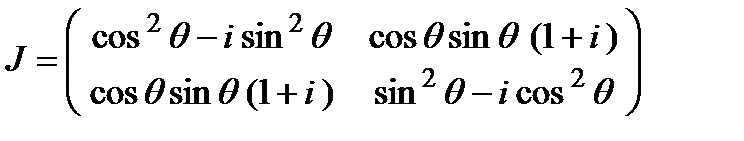
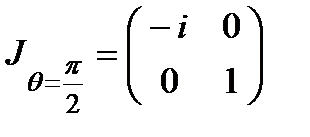
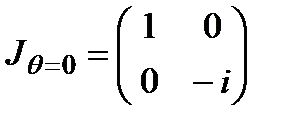
в. Оптический вращатель, поворачивающий плоскость поляризации на угол 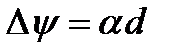 , где
, где 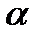 – вращательная способность оптически активного кристалла,
– вращательная способность оптически активного кристалла, 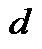 – толщина кристалла:
– толщина кристалла:
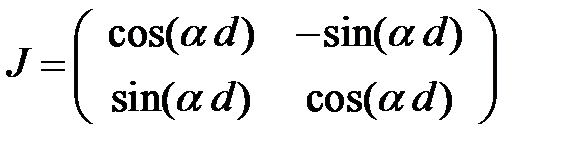
Вращательная способность определяется выражением
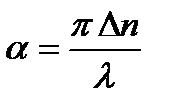
где 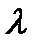 – длина волны света в вакууме;
– длина волны света в вакууме; 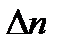 – разность показателей преломления для право- и лево- циркулярно поляризованного света.
– разность показателей преломления для право- и лево- циркулярно поляризованного света.
В системе координат х О у, действие поляризационного элемента, заданного в системе координат 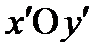 , повернутой на угол
, повернутой на угол 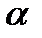 , описывается следующим образом:
, описывается следующим образом:

6. Найти интенсивность света, прошедшего через кристаллическую пластину, вносящую разность фаз 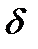 между обыкновенным и необыкновенным лучами, если пластинка находится между двумя идеальными поляризаторами, плоскости поляризации которых составляют углы
между обыкновенным и необыкновенным лучами, если пластинка находится между двумя идеальными поляризаторами, плоскости поляризации которых составляют углы 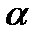 и
и 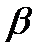 с быстрой осью пластинки. Исследовать случаи скрещенного и параллельного положения плоскостей поляризации поляризаторов.
с быстрой осью пластинки. Исследовать случаи скрещенного и параллельного положения плоскостей поляризации поляризаторов.
Решение:
Введем систему координат х О у, оси которой совпадают с быстрой и медленной осями кристаллической пластинки, и систему 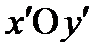 , ось
, ось 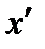 которой совпадает с главной плоскостью первого поляризатора (рис. 6.5), Тогда вектор Джонса излучения, прошедшего через первый поляризатор в системе
которой совпадает с главной плоскостью первого поляризатора (рис. 6.5), Тогда вектор Джонса излучения, прошедшего через первый поляризатор в системе 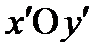 , имеет вид:
, имеет вид:
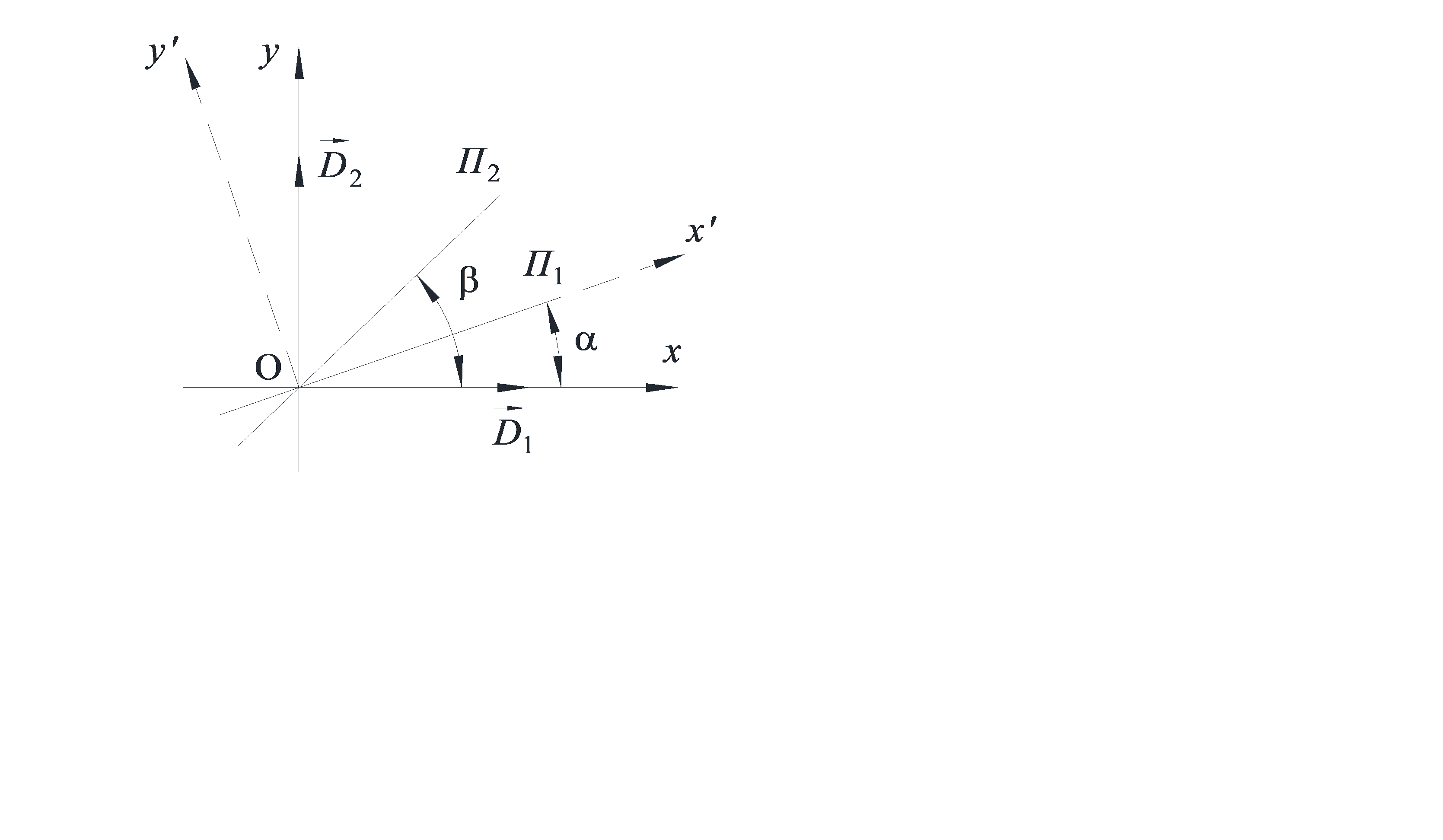
Рис 6.5.
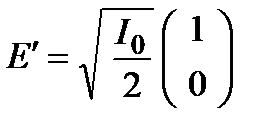 ,
,
где 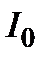 – интенсивность излучения на входе поляризатора
– интенсивность излучения на входе поляризатора 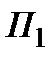 .
.
Этот вектор в системе координат х О у будет иметь следующий вид:
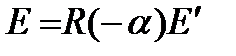 .
.
Используя последовательно (6.14), матрицы кристаллической пластины (6.16) при азимуте, равном 0, а также матрицу поляризатора (6.15), для вектора Джонса получаем следующее выоажени:
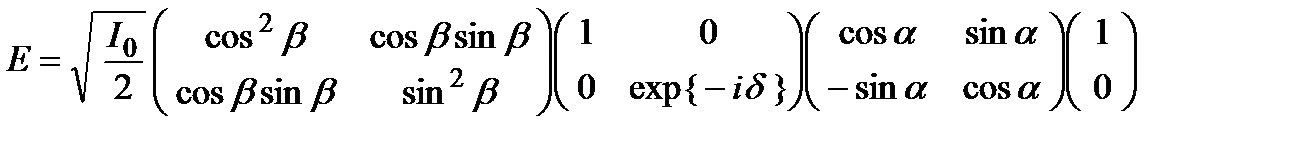
После перемножения матриц получаем:
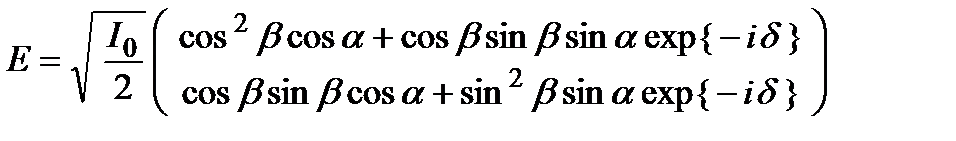
Следовательно, интенсивность излучения на выходе:
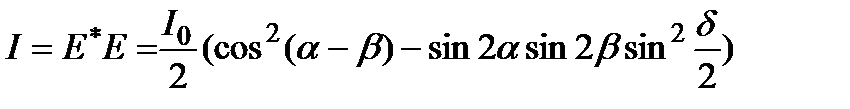
Если плоскости поляризации поляризаторов параллельны (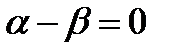 ),
),
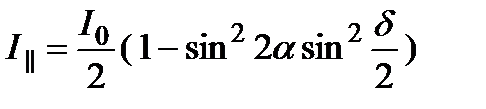 .
.
Если плоскости поляризации поляризаторов скрещены (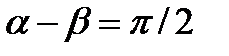 ),
),
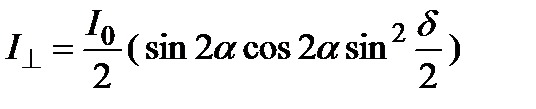 .
.
7. Линейно поляризованный свет проходит через кристаллическую фазосдвигающую пластинку. Известно, что плоскость поляризации составляет угол 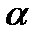 с осью
с осью 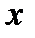 , совпадающей с одним из главных направлений пластинки, а вносимый ею фазовый сдвиг равен
, совпадающей с одним из главных направлений пластинки, а вносимый ею фазовый сдвиг равен 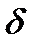 (рис. 6.6). Показать, что на выходе из пластинки свет будет эллиптически поляризованным; найти угол, который образуют оси этого эллипса с осью
(рис. 6.6). Показать, что на выходе из пластинки свет будет эллиптически поляризованным; найти угол, который образуют оси этого эллипса с осью 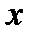 , и отношение длин осей эллипса.
, и отношение длин осей эллипса.
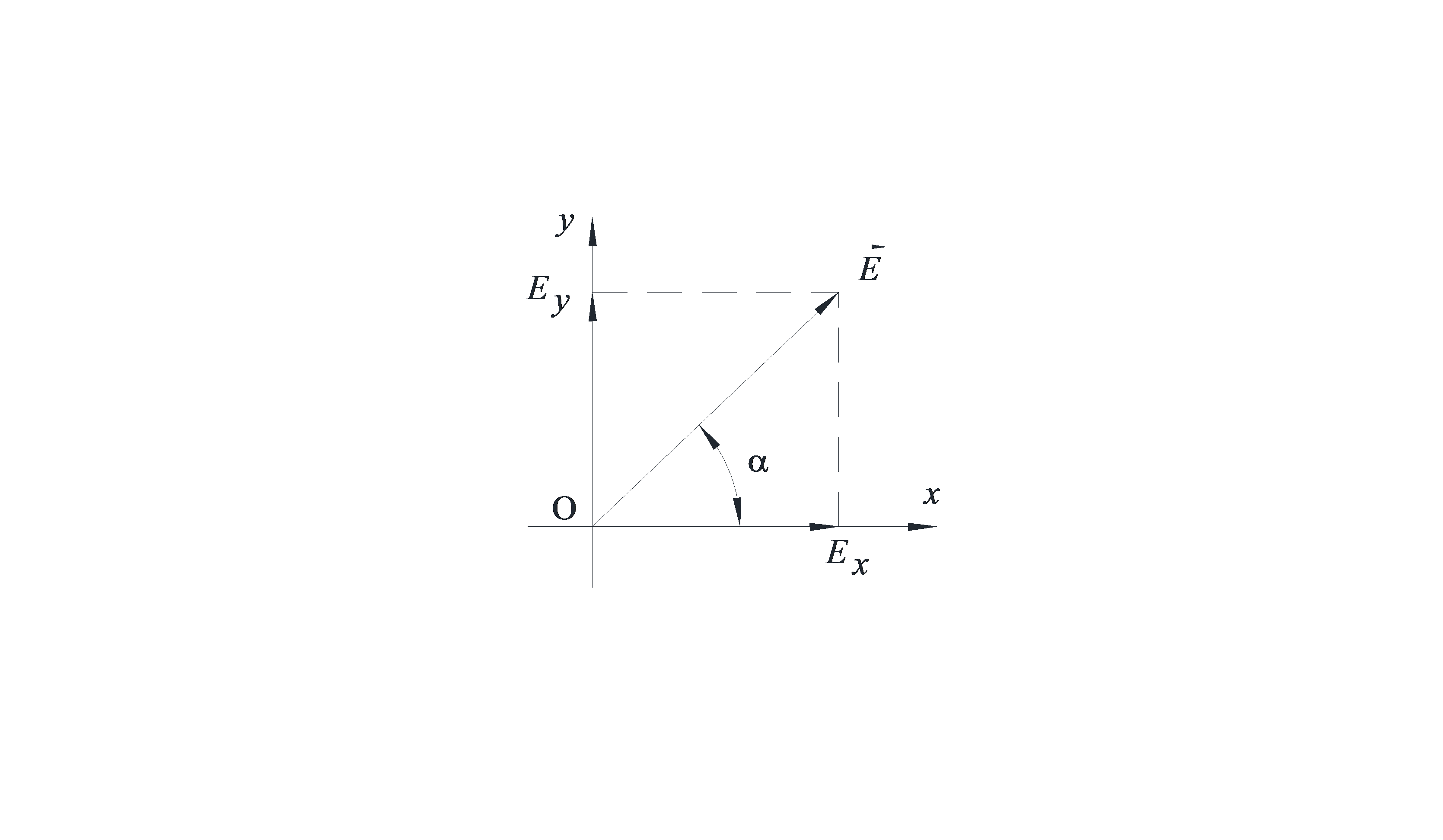
Рис 6.6.
Решение:
Считая интенсивность пучка равной единице, запишем вектор Джонса на входе кристаллической пластинки:
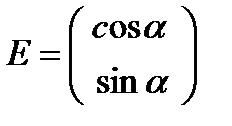
Пусть быстрая ось пластинки совпадает с осью  , тогда вектор Джонса на выходе пластины будет иметь вид:
, тогда вектор Джонса на выходе пластины будет иметь вид:
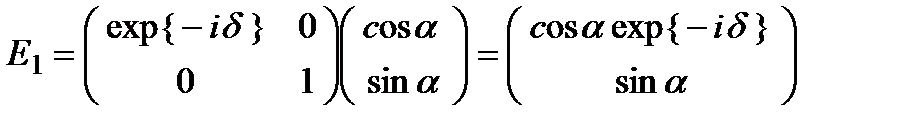
Полученный вектор Джонса соответствует эллиптически поляризованному свету.
Для нахождения ориентации и отношения осей эллипса поляризации пропустим излучение через поляризатор, главная плоскость которого составляет произвольный угол 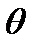 с осью
с осью 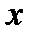 . Тогда на выходе поляризатора получим:
. Тогда на выходе поляризатора получим:
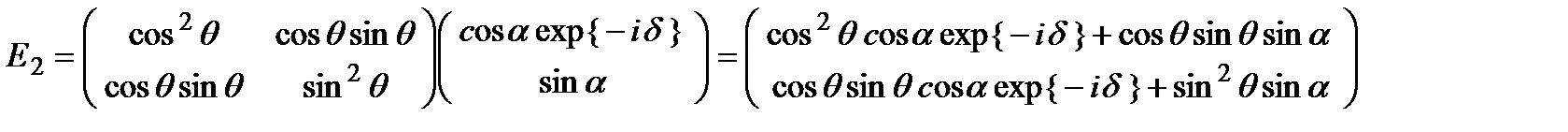
Переходя к интенсивности получаем:
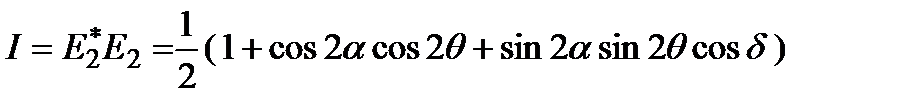
Полученное выражение показывает, что интенсивность является функцией угла 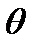 , и при углах
, и при углах 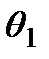 и
и 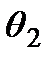 , совпадающих с осями эллипса, принимает экстремальные значения. Поэтому условием для нахождения
, совпадающих с осями эллипса, принимает экстремальные значения. Поэтому условием для нахождения 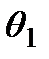 и
и 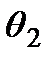 является равенство нулю производной
является равенство нулю производной 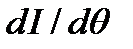 .
.
Решив уравнение
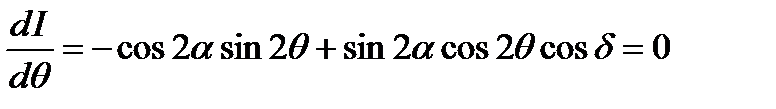
получим:
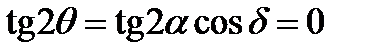 (6.17)
(6.17)
Удовлетворяющие уравнению (6.17) значения 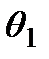 и
и 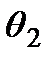 отличаются на
отличаются на 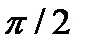 , т.е.
, т.е.
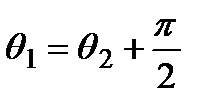
а соответственно значения 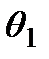 и
и 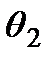 соответствуют взаимно перпендикулярным осям эллипса.
соответствуют взаимно перпендикулярным осям эллипса.
Для определения отношения осей эллипса 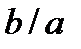 необходимо найти отношение
необходимо найти отношение 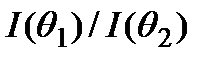 , которое равно
, которое равно 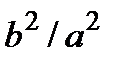 :
:
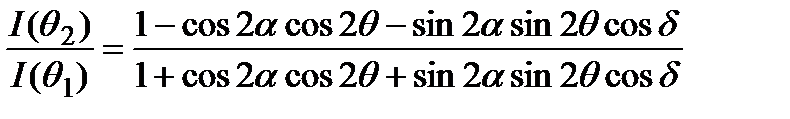
Используем соотношение (6.17) после преобразования получаем:
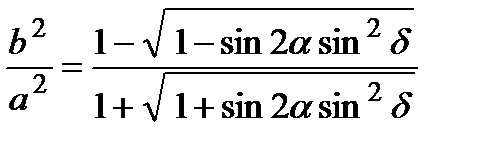 (6.18)
(6.18)
Отношение полуосей эллипса представляют в виде тангенса некоторого угла 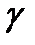 , т.е.
, т.е. 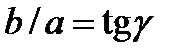 . Из (6.18) легко получить:
. Из (6.18) легко получить:
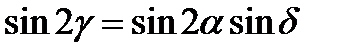
Задачи для самостоятельного решения
1. Определить скорости распространения и показатели преломления обыкновенной и необыкновенной волн в отрицательном одноосном кристалле, если 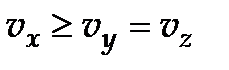 .
.
Ответ: 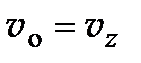 ,
, 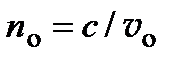 .
.
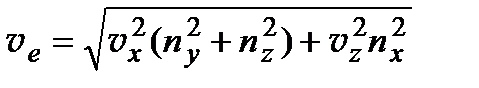 ,
, 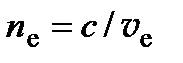
 2020-05-12
2020-05-12 465
465








