2020-05-12
94
Рассмотрим изолированную особую точку 
однозначной аналитичекой функции 
В проколотой окрестности точки
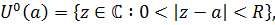
в которой функция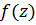 
аналитична, возьмем замкнутый контур 
содержащий внутри себя точку
Тогда в ычетом функции 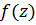в точке называется интеграл
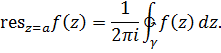
Замечание.
В силу теоремы Коши этот интеграл не зависит от замкнутого контура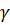 
, лежащего в проколотой окрестности точки и содержащего эту точку внутри себя.
Квант. 08.02.02. Вычисление вычета (Т)
Рассмотрим изолированную особую точку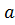 
однозначной аналитичекой функции
Пусть
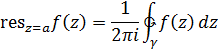
Тогда
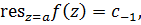
где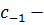 
коэффициент при 
в разложении Лорана.
Доказательство.
В окрестности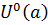 
функция представляется равномерно сходящимся рядом Лорана
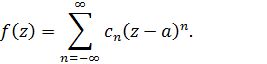
Интегрируя этот ряд почленно, и учитывая, что
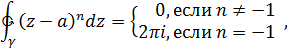
получим
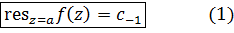
Квант. 08.02.03. Вычет функции в бесконечно удаленной изолированной особой точке (О)
Рассмотрим бесконечно удаленную изолированную особую точку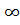 
однозначной аналитической функции
В проколотой окрестности точки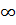 
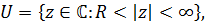
в которой функция 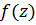аналитична, возьмем замкнутый контур вне которого функция аналитична
Тогда в ычетом функции 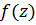в бесконечно удаленной точке 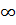называется интеграл
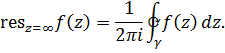
Интегрирование по контуру 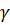осуществляется в положительном направлении относительно ограничиваемой им области (содержащей бесконечно удаленную точку), т. е. по часовой стрелке.
Квант. 08.02.04. Вычисление вычета в бесконечно удаленной точке (Т)
Рассмотрим бесконечно удаленную изолированную особую точку 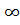однозначной аналитической функции
Пусть
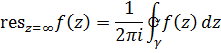
Тогда
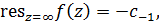
где 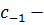коэффициент при 
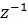в разложении Лорана.
Доказательство.
Такое же, как для конечной точки.
Замечание.
Из формулы (1) следует, что вычет функции в устранимой особой точке равен нулю, если точка лежит в конечной части плоскости. В случае бесконечно удаленной точки это не так, поскольку коэффициент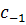 
принадлежит правильной части разложения Лорана.
Пример.
В кольце
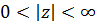
которое одновременно является проколотой окрестностью нуля и окрестностью бесконечно удаленной точки, имеем разложение
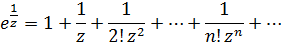
Из этого разложения видно, что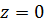 
является существенно особой точкой, a 
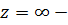устранимой и что коэффициент 
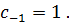Поэтому
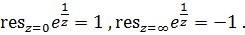
В случае полюса имеются формулы для вычисления вычета, не требующие знать разложение Лорана.
