2020-05-12
95
Рассмотрим однозначную аналитическую в 
функцию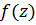 
Пусть
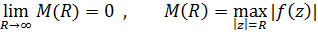
Тогда
где 
верхняя и 
нижняя половинки окружности
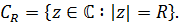
Доказательство.
Пусть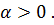 
Учитывая неравенство
оценим интеграл
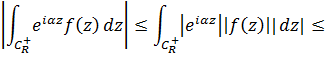
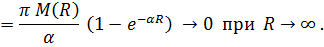
Лемма Жордана доказана.
Пример. Вычислить интеграл
Этот интеграл сходится условно. Вычислим его, используя лемму Жордана и формулу Эйлера
Рассмотрим функцию 
Эта функция не имеет особых точек в верхней полуплоскости, но имеет полюс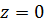 
на действительной оси. Поэтому возьмем замкнутый контур, состоящий из отрезков 
верхней полуокружности 
, проходимой по часовой стрелке и верхней полуокружности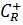 
, проходимой против часовой стрелки (см. рис.).
Внутри этого контура нет особых точек функции, поэтому интеграл по контуру в силу теоремы Коши равен нулю:
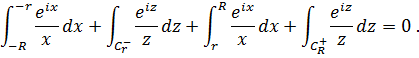
Устремим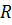 
к бесконечности, а 
- к нулю. Тогда
Найдем предел
Подынтегральная функция разлагается в ряд Лорана в проколотой окрестности нуля
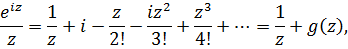
где
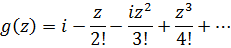
аналитическая в окрестности нуля функция и, следовательно, ограниченная в этой окрестности
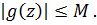
Имеем
Следовательно
