2020-05-12
86
Рассмотрим однозначную аналитическую функцию 
и ее изолированную особую точку 
Пусть
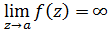
Тогда точка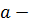 
полюс функции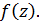 
Доказательство.
Пусть в изолированной особой точке предел функции равен бесконечности
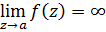
тогда для функции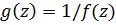 
имеем
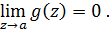
Доопределяя функцию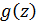 
в точке , положим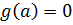 
. Тогда функция 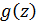будет иметь в точке нуль, а функция 
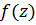будет иметь в точке полюс.
Квант. 08.01.09. Поведение функции в окрестности существенно особой точки (Т)
Рассмотрим однозначную аналитическую функцию
Пусть 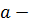ее существенно особая точка
Тогда не существует ни конечного и бесконечного предела функции в этой точке.
Доказательство.
Так как в противном случае эта точка была бы устранимой или полюсом.
Пример.
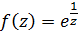
Особая точка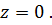 
Разложение Лорана в проколотой окрестности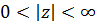 
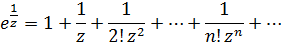
Главная часть содержит бесконечно много членов, т.е.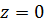 
существенно особая точка. В этом можно убедиться и по отсутствию предела при 
:
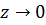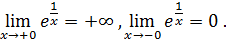
Таким образом, мы можем классифицировать особые точки по поведению функции в их окрестности.
|
|
|
Квант. 08.01.10. Классификация изолированных особых точек по поведению функции (О)
Рассмотрим изолированную особую точку однозначной аналитичекой функции
Пусть
1. существует конечный
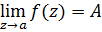
2.
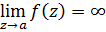
3. не существует
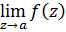
Тогда соответственно точка является
1. устранимой особой точкой
2. полюсом
3. существенно особой точкой
Замечание.
Бесконечно удаленная точка всегда считается особой. Характер особенности определяется по поведению функции при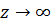 
так же как и для конечных точек.
Квант. 08.01.11. Бесконечно удаленная изолированная особая точка (О)
Рассмотрим однозначную функцию
Пусть она аналитична в некоторой окрестности бесконечно удаленной точки
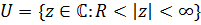
Тогда бесконечно удаленная точка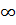 
является изолированной особой точкой.
