2020-05-12
78
Рассмотрим изолированную особую точку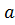 
, которая является полюсом 
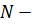го порядка для однозначной аналитичекой функции 
Пусть
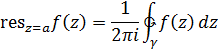
Тогда
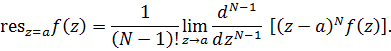
В частности для простого полюса (
имеем
Доказательство.
Пусть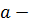 
полюс 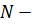го порядка функции 
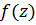. Ее разложение Лорана в окрестности полюса
Нам нужно найти коэффициент 
Для этого умножим разложение на 
и продифференцируем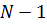 
раз.
Переходя к пределу при 
, получим искомый коэффициент.
В частности, для простого полюса ( имеем
Квант. 08.02.06. Вычисление вычета относительно простого полюса для частного двух функций (Т)
Рассмотрим изолированную особую точку 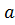, которая является простым полюсом для однозначной аналитичекой функции
Пусть
Тогда
Доказательство.
Рассмотрим случай, когда функция представляется в виде частного и имеет в точке 
простой полюс, т.е.
Тогда
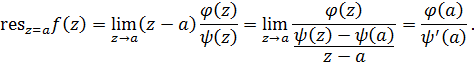
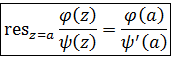
Пример. 
Особые точки – это нули знаменателя. Найдем их.
Таким образом, все нули косинуса 
лежат на действительной оси. Поскольку 
, то 
простые полюсы тангенса и вычеты в них равны
|
|
|
Квант. 08.02.07. Основная теорема о вычетах (Т)
Рассмотрим замкнутый контур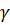 
, который лежит в области аналитичности функции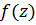
Пусть внутри контура 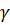имеется конечное число особых точек 
функции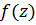
Тогда
Доказательство.
Вырежем особые точки замкнутыми контурами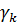 
, которые не пересекаются друг с другом и все лежат внутри контура 
Тогда по теореме Коши для многосвязной области
Теорема доказана.
Квант. 08.02.08. Вторая теорема о вычетах (Т)
Рассмотрим однозначную аналитическую функцию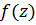
Пусть функция 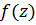имеет конечное число особых точек в плоскости 
Тогда
Доказательство.
Если функция 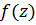имеет конечное число особых точек в плоскости , то выбрав замкнутый контур 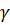, содержащий внутри себя все особые точки, получим
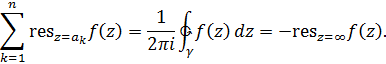
Таким образом
