2020-05-12
86
Найти вычеты данных функций относительно всех особых точек, включая бесконечно удаленную.
1.
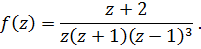
Решение. О собые точки
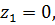простой полюс,
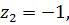простой полюс,
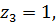полюс 3-го порядка,
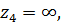устранимая особая точка (нуль четвертого порядка).
1)
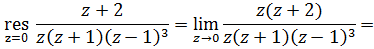
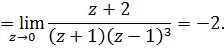2)
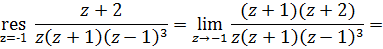
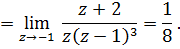
3)
Поскольку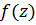 
имеет в бесконечно удаленной точке нуль 4-го порядка,
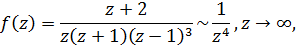
то это означает, что в разложении Лорана отсутствует член
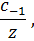
то есть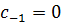 
и, следовательно,
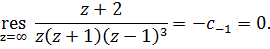
4)Вычет в точке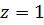 
можно найти по формуле
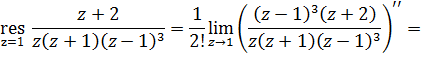
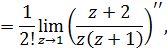
или воспользоваться второй теоремой о вычетах:
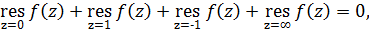
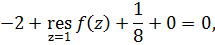
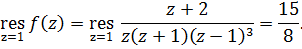
2.
Решение. Особые точки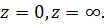 
Разложение Лорана в кольце
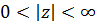, которое является проколотой окрестностью и нуля и бесконечно удаленной точки, имеет вид
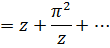
Следовательно,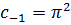 
и
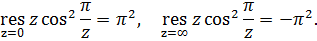
Отметим, что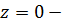 
существенно особая точка, 
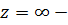полюс первого порядка.
Вычислить интегралы по замкнутому контуру.
3.
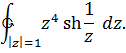
Решение. Особые точки 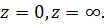Внутри контура лежит одна особая точка 
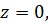поэтому
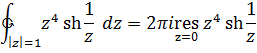
Разложение подынтегральной функции в ряд Лорана в кольце 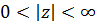, которое является проколотой окрестностью и нуля и бесконечно удаленной точки, имеет вид
|
|
|
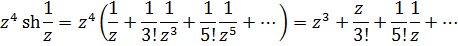
Следовательно,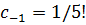 
и
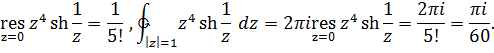
Отметим, что 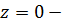существенно особая точка.
4.
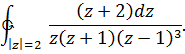
Решение. Особые точки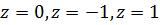 
лежат внутри контура, вне контура лежит только одна особая точка 
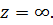Поэтому
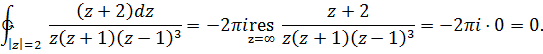
Параграф 3.Применение вычетов для вычисления интегралов.
Существуют только два метода точного вычисления интегралов (кроме непосредственного вычисления по определению как предела интегральных сумм)- по формуле Ньютона-Лейбница и с помощью вычетов.
Интегралы от аналитических функций по замкнутому контуру вычисляются по формуле (2). Если нужно вычислить интеграл по незамкнутому контуру, то делают преобразования, сводящие вычисление этого интеграла к вычислению интеграла по замкнутому контуру. Как это делается рассмотрим на примерах.
Примеры.
1) Вычислить интеграл
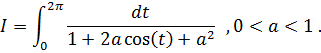
Делаем замену переменной
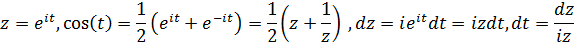
Получаем
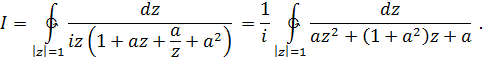
Многочлен
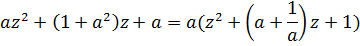
имеет два корня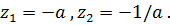 
В круге 
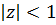лежит корень 
и является простым полюсом подынтегральной функции
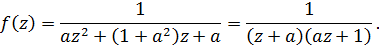
Вычет в этом полюсе равен
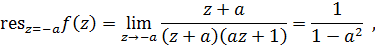
и интеграл по основной теореме о вычетах
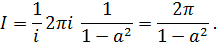
2) Вычислить интеграл
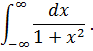
Этот интеграл абсолютно сходится. Функция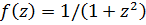 
является аналитической в комплексной плоскости, за исключением точек 
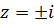, которые являются для нее простыми полюсами, а на действительной оси она совпадает с подынтегральной функцией. Возьмем окружность
которая содержит внутри себя полюс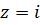 
, лежащий в верхней полуплоскости. Обозначим 
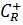ее верхнюю половину, проходимую против часовой стрелки. Для замкнутого контура, состоящего из отрезка 
действительной оси и полуокружности 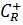по основной теореме о вычетах имеем
|
|
|
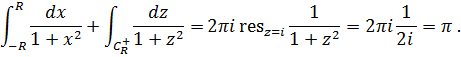
Устремим теперь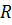 
к бесконечности. Получим
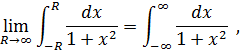
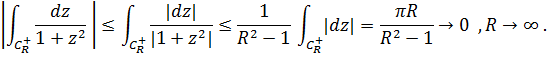
Таким образом
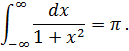
Аналогично можно использовать особые точки, лежащие в нижней полуплоскости, взяв нижнюю полуокружность 
, проходимую по часовой стрелке.
Замечание.
Указанный прием применим к интегралам вида
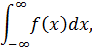
где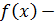 
аналитически продолжается с действительной оси в верхнюю или нижнюю полуплоскость, имеет там конечное число особых точек и на бесконечности убывает по модулю достаточно быстро
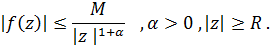
Это условие обеспечивает стремление к нулю интеграла по полуокружности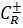 
:
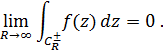
Для вычисления интегралов вида
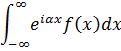
Нам потребуется лемма Жордана.
