2020-05-12
100
Теорема (о замене переменной в определённом интеграле). Пусть функция y = f (x) непрерывна на [ a, b ]. Если функция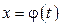 
имеет непрерывную производную на отрезке 
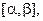при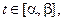 
значение функции 
и, кроме того, 
то справедлива формула
(9)
Алгоритм замены переменной в определённом интеграле:
1. Старую и новую переменные связать соотношением ;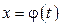
2. Найти связь между дифференциалами переменных x и t: 
3. Определить новые пределы интегрирования α и β из уравнений 
4. В искомом интеграле перейти к новой переменной по формуле (9) и заменить пределы интегрирования. Проинтегрировать и вычислить по формуле Ньютона–Лейбница (8).
Пример. Вычислить определённый интеграл 
Решение.
Интегрирование по частям в определённом интеграле
Формула интегрирования по частям (3) в случае определённого интеграла приобретает вид:
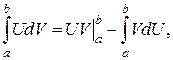(10)
Пример. Вычислить определённый интеграл 
Решение.
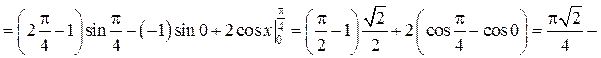
Приложения определённого интеграла
Определённый интеграл используется в различных приложениях: при вычислении площадей плоских фигур, длин дуг плоских кривых, объемов тел вращения, площадей поверхностей вращения, работы переменной силы на отрезке, пути, пройденного за промежуток времени, статических моментов и моментов инерции плоских дуг и фигур и т. д.
Площади плоских фигур
