Рассмотрим некоторые из интегралов от тригонометрических функций. Виды интегралов и способы их вычисления приведем в табл. 2.
Таблица 2.
| Вид интеграла | Метод интегрирования |
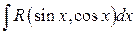 Общий случай
Общий случай
| Замена 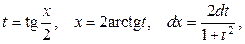
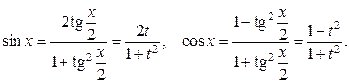
|
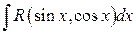 , где , где
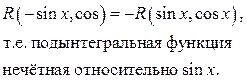
| Замена 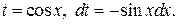
|
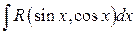 , где , где
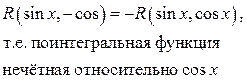
| Замена 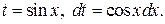
|
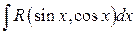 , где , где
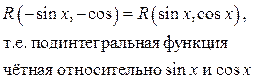
| Замена 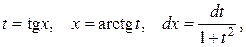
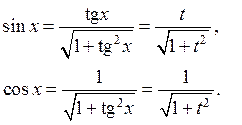
|
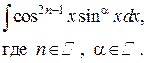
| Замена 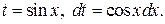 Если
Если 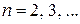 , то необходимо учитывать формулу , то необходимо учитывать формулу 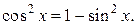
|
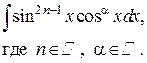
| Замена 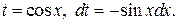 Если
Если 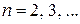 , то необходимо учитывать формулу , то необходимо учитывать формулу 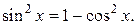
|
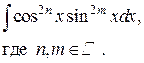
| Использовать формулы понижения степени:
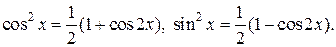
|
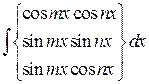
| Использовать формулы преобразования произведения тригонометрических функций в сумму:
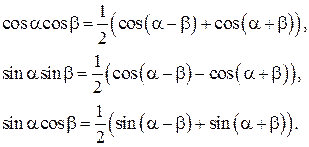
|
Пример. Найти интегралы:

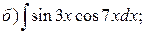
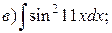
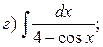
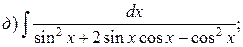
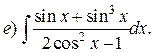
Решение.
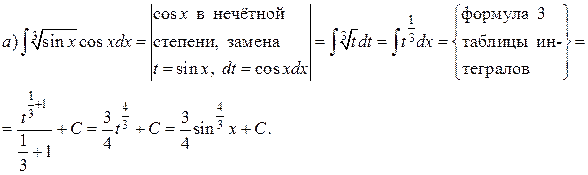
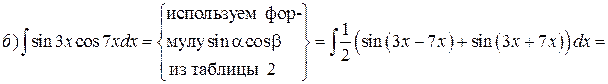
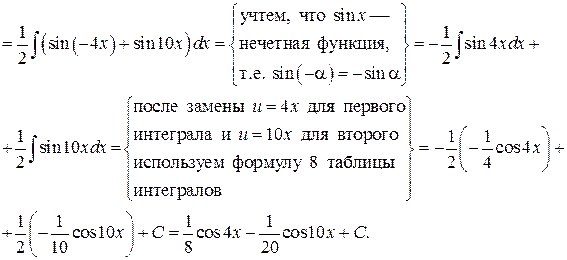
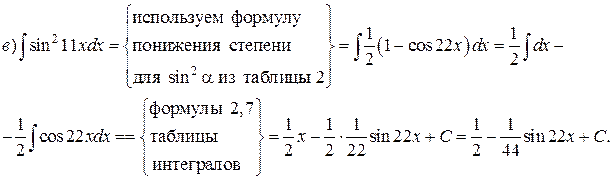
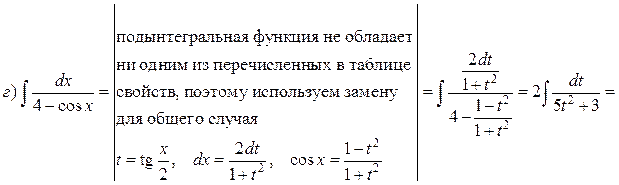
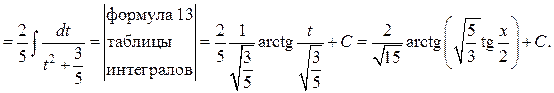
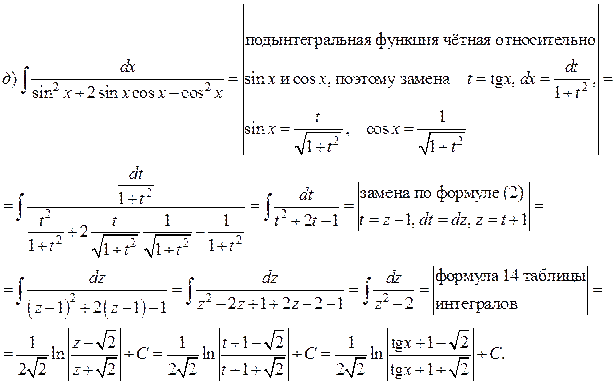
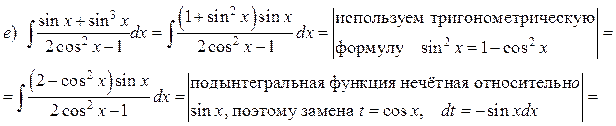
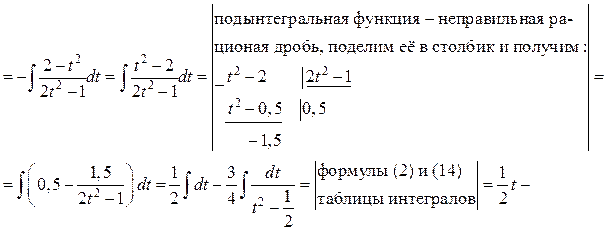
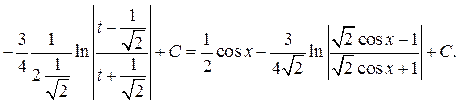
Интегрирование простейших иррациональных функций
Определение. Иррациональностью от 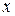 называют выражение, содержащее переменную
называют выражение, содержащее переменную 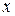 в дробной степени.
в дробной степени.
Рассмотрим интеграл
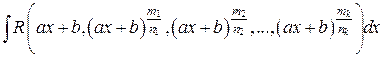 ,
,
где R 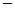 рациональная функция по каждой из своих переменных; m 1, n 1, m 2, n 2,...
рациональная функция по каждой из своих переменных; m 1, n 1, m 2, n 2,...  целые числа.
целые числа.
Подстановка, рационализирующая подынтегральную функцию, имеет вид:
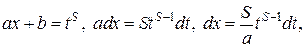
где S 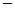 наименьшее общее кратное (НОК) чисел
наименьшее общее кратное (НОК) чисел 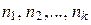 , т. е. наименьшее натуральное число, делящееся нацело на
, т. е. наименьшее натуральное число, делящееся нацело на 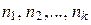 .
.
Пример. Проинтегрировать иррациональность 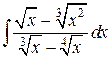 .
.
Решение.

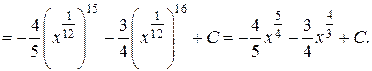
Тригонометрические подстановки
Рассмотрим интегралы, которые приводятся к интегралам от рациональной относительно 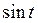 и
и 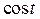 функции с помощью надлежащей тригонометрической подстановки. Виды интегралов и способы их вычисления приведем в табл. 3.
функции с помощью надлежащей тригонометрической подстановки. Виды интегралов и способы их вычисления приведем в табл. 3.
Таблица 3.
| Вид интеграла | Подстановка |
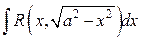
| 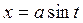 , , 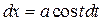 или или 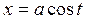 , , 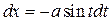
|
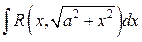
| 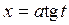 , , 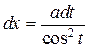 или или 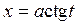 , , 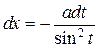
|
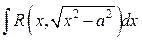
| 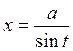 , , 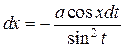 или или 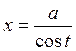 , , 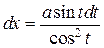
|
Пример. Найти интегралы
а) 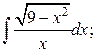 б)
б) 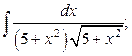 в)
в) 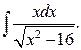
Решение.
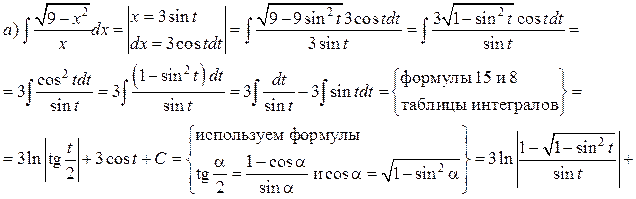
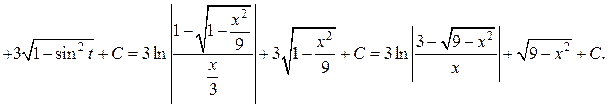
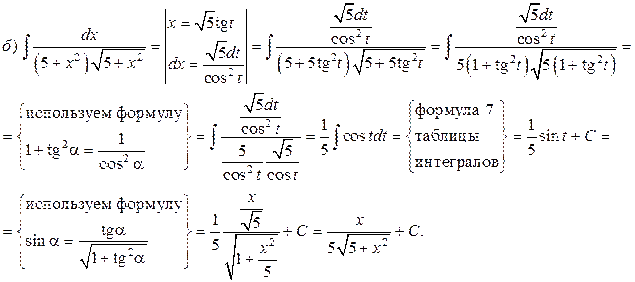
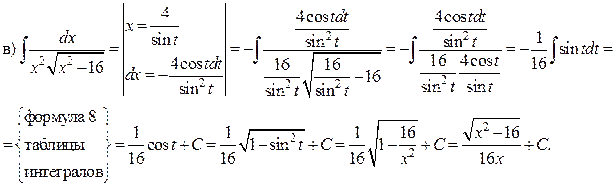
ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ
 2020-05-12
2020-05-12 148
148








