2020-05-12
166
Теорема. Если плоская фигура (рис. 1) ограничена линиями 
, где 
для всех 
, и прямыми
, 
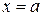, то её площадь вычисляется по формуле:
(11)
Пример. Найти площадь фигуры, ограниченной линиями:
| 
|
| Рис. 1 | Рис. 2 |
Решение. Построим схематический рисунок (рис. 2). Для построения параболы найдём координаты её вершины 
и направим верви параболы вверх. Для построения прямой достаточно двух точек, например 
и 
.
Площадь S фигуры, ограниченной обеими линиями (она отмечена на рис. 2 штриховкой) вычислим согласно формуле (11). Для определения нижнего и верхнего пределов интегрирования в этой формуле составим и решим уравнение 
Итак, имеем 
Площадь полученной фигуры найдем по формуле (11), при 
(поскольку 
для всех 
), получаем:
Вычисление площадей фигур, ограниченных линиями, заданными
Параметрически
Площадь криволинейной трапеции, ограниченной сверху кривой, заданной параметрически уравнениями 
где функции 
и 
имеют непрерывные производные для всех 
, и функция y (t) сохраняет знак на промежутке 
прямыми x = a, x = b, где a = x (t 0), b = x (t 1), и осью OX, вычисляется по формуле:
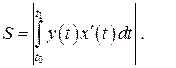(12)
Пример. Найти площадь фигуры, ограниченной линиями, заданными параметрически: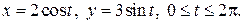 
Решение.
Для построения фигуры составим таблицу значений координат (x, y)
точек кривой, соответствующих различным значениям параметра 
| t | 0 | 
| 
| 
| 
|
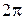
| x | 2 | 0 | –2 | 0 | 2 |
| y | 0 | 3 | 0 | –3 | 0 |
|
| Рис. 3 |
Нанесём точки (x, y) на координатную плоскость XOY и соединим их плавной линией. Когда параметр 
изменяется от 
до 
, соответствующая точка 
описывает эллипс (известно, что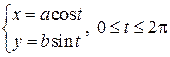 
– параметрические формулы, задающие эллипс с полуосями a и b). Учитывая симметрию фигуры относительно координатных осей OX и OY, найдём её площадь S, умножив на 4 площадь криволинейной трапеции AOB. Согласно формуле (12) получим:
Заметим, что для вычисления площади по формуле (9), построение чертежа не является обязательным, а носит иллюстративный характер.
Длина дуги плоской кривой
Вычисление длины дуги плоской кривой в декартовых
Координатах
Если кривая задана уравнением 
, функция 
имеет непрерывную производную при всех , то длина дуги 
(рис. 4) этой кривой, заключённой между точками 
и 
|
| Рис. 4 |
вычисляется по формуле:
(13)
