Свойства определённого интеграла

Замечание. Свойство 3 справедливо при любом расположении точки с по отношению к а и b при условии интегрируемости функции f (x) на большем из отрезков.

6) Если для всех , то

7) Если для всех , то справедлива оценка

8) Теорема (о среднем значении функции на отрезке). Если функция непрерывна на отрезке [ a,b ], то между точками а и b найдётся точка х = с, такая что

Определение. Средним значением функции 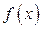на отрезке [ a,b ] называется величина

Формула Ньютона–Лейбница

Теорема (о производной от интеграла с переменным верхним пределом). Пусть функция непрерывна на [ a,b ], тогда производная от определённого интеграла с переменным верхним пределом равна значению подынтегральной функции на этом верхнем пределе:

Доказательство. Обозначим Придадим переменной х приращение тогда получит приращение где с – некоторая точка между х и По определению производной имеем причём последнее равенство справедливо ввиду непрерывности функции

Следствие. первообразная для функции .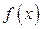

Теорема (формула Ньютона–Лейбница). Если функция 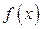непрерывна на отрезке [ a,b ], то справедлива формула

(8)

где любая первообразная для функции 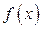, т.е.,

Доказательство. По следствию из предыдущей теоремы первообразная для функции 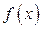. По теореме о первообразной для данной функции любая другая первообразная отличается от на постоянное слагаемое: