Определённый интеграл, теорема его существования

Рассмотрим функцию 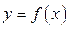, которая непрерывна на отрезке [ a,b ]. Выполним следующие операции:

1. Отрезок [ a,b ]  разобьём точками 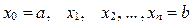 на n произвольных частей и обозначим длины отрезков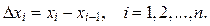

2. Внутри каждого отрезка 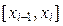 возьмём произвольную точку С_i  и вычислим в ней значение функции  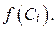Составим сумму произведений значений функции  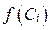на  

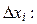
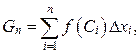                                       (5)

называемую интегральной суммой для функции 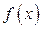 на отрезке [ a,b ].

3. Обозначим 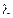 длину наибольшего из отрезков разбиений 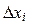, т.е.,  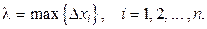В равенстве (5) перейдём к пределу при :

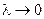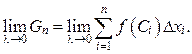                                    (6)

Определение. Если существует конечный предел при 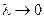 интегральной суммы, составленной для функции  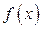на отрезке [ a,b ], не зависящий ни от способа разбиения [ a,b ] на части, ни от выбора произвольной точки С_i внутри каждого частичного отрезка разбиения, то этот предел называется определённым интегралом от функции 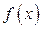на отрезке [ a,b ]. Обозначение определённого интеграла:

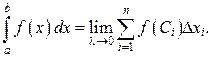                              (7)

При этом а называется нижним пределом, а b   верхним пределом интегрирования.

Если функция 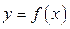 непрерывна и неотрицательна на отрезке [ a,b ], то определённый интеграл от функции 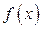на этом отрезке имеет геометрический смысл. Приведём геометрическую интерпретацию определённого интеграла.

Определение. Криволинейной трапецией называется плоская фигура, ограниченная сверху графиком функции 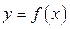, снизу отрезком [ a,b ] оси ОХ и двумя прямыми х=а и х=b, параллельными оси ОY.

Можно показать, что площадь криволинейной трапеции с основанием [ a,b ] и ограниченной сверху графиком функции 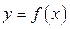, непрерывной и неотрицательной на отрезке [ a,b ], равна определённому интегралу от функции  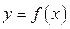на этом отрезке, т.е.:

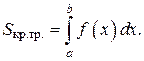
Теорема (существования определённого интеграла). Если функция 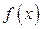 непрерывна на отрезке [ a,b ], то существует определённый интеграл от этой функции на отрезке [ a,b ].