Согласно определению ДУ n -го порядка имеют вид (21). Будем рассматривать уравнения, разрешённые относительно старшей производной:
 (33)
(33)
Одним из способов интегрирования таких уравнений является понижение порядка. Рассмотрим несколько частных случаев.
I. ДУ вида 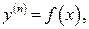 т. е. правая часть является функцией одной переменной x. Такие ДУ решаются последовательным интегрированием n раз. Следовательно, полученное решение будет содержать n произвольных постоянных С 1, С 2,…, С n. Такое решение будем называть общим. Фиксируя произвольные постоянные, будем получать решения, называемые частными.
т. е. правая часть является функцией одной переменной x. Такие ДУ решаются последовательным интегрированием n раз. Следовательно, полученное решение будет содержать n произвольных постоянных С 1, С 2,…, С n. Такое решение будем называть общим. Фиксируя произвольные постоянные, будем получать решения, называемые частными.
Пример. Найти общее решение ДУ 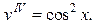
Решение. Согласно определению производная четвёртого порядка является производной от производной третьего порядка, следовательно, уравнение можно переписать в виде  Умножим обе части уравнения на dx и получим
Умножим обе части уравнения на dx и получим  Проинтегрируем полученное равенство, при этом используем для
Проинтегрируем полученное равенство, при этом используем для 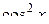 формулу понижения степени, и получим:
формулу понижения степени, и получим:

Аналогично получим интегрированием 
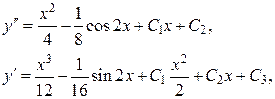

II. ДУ вида  где
где  Это уравнение допускает понижение порядка на k единиц с помощью постановки
Это уравнение допускает понижение порядка на k единиц с помощью постановки  где
где  тогда
тогда  и уравнение примет вид
и уравнение примет вид  Если его удастся проинтегрировать, то найдём
Если его удастся проинтегрировать, то найдём  или
или 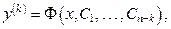 а это – уравнение типа I.
а это – уравнение типа I.
Пример. Найти общее решение ДУ 
Решение. Это уравнение не содержит  поэтому допускает понижение порядка на две единицы путём постановки
поэтому допускает понижение порядка на две единицы путём постановки  В результате получим ДУ первого порядка
В результате получим ДУ первого порядка  Это ДУ с разделяющимися переменными. Подставляя в уравнение
Это ДУ с разделяющимися переменными. Подставляя в уравнение  и разделяя переменные, получаем
и разделяя переменные, получаем 
После интегрирования имеем:  где
где 
Учитывая, что  получим
получим  Это ДУ типа I, решаем его последовательным интегрированием:
Это ДУ типа I, решаем его последовательным интегрированием:

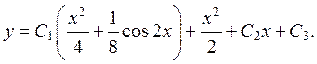
III. ДУ вида  Это уравнение допускает понижение порядка на одну единицу, если сделать замену переменной: у – новая независимая переменная, а
Это уравнение допускает понижение порядка на одну единицу, если сделать замену переменной: у – новая независимая переменная, а 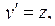 где
где  новая искомая функция. Найдём
новая искомая функция. Найдём 
 Очевидно, что
Очевидно, что  будет выражаться через
будет выражаться через  и уравнение примет вид
и уравнение примет вид  Если удастся это уравнение проинтегрировать, то получим
Если удастся это уравнение проинтегрировать, то получим  или
или  а это ДУ первого порядка с разделяющимися переменными.
а это ДУ первого порядка с разделяющимися переменными.
Пример. Найти общее решение ДУ 
Решение. Применяя замену  получаем
получаем  Это уравнение с разделяющимися переменными. Подставляя
Это уравнение с разделяющимися переменными. Подставляя  и разделяя переменные, получаем:
и разделяя переменные, получаем:  После интегрирования получим:
После интегрирования получим:  и
и  или
или  Заменяя
Заменяя  и разделяя переменные, получаем:
и разделяя переменные, получаем:  После интегрирования находим общий интеграл ДУ:
После интегрирования находим общий интеграл ДУ:
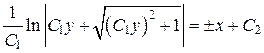 или
или 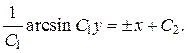
Добавим также, что уравнение имеет особое решение  которое не получается из общего интеграла уравнения и соответствует случаю
которое не получается из общего интеграла уравнения и соответствует случаю 
3.8. Задача Коши для дифференциальных уравнений
высших порядков
Для дифференциального уравнения порядка n задача Коши ставится следующим образом: найти такое решение  уравнения (33), которое удовлетворяло бы условиям:
уравнения (33), которое удовлетворяло бы условиям: 
 где
где  некоторые заданные значения.
некоторые заданные значения.
Теорема (существования и единственности решения задачи Коши для ДУ порядка n). Пусть в уравнении (33) функция 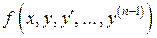 непрерывна в некоторой области D
непрерывна в некоторой области D  мерного пространства, а все частные производные
мерного пространства, а все частные производные  ограничены в этой области. Тогда существует единственное решение
ограничены в этой области. Тогда существует единственное решение  уравнения (33), определённое и непрерывное в некоторой окрестности точки
уравнения (33), определённое и непрерывное в некоторой окрестности точки  и удовлетворяющее условиям:
и удовлетворяющее условиям: 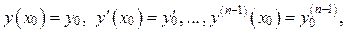 где
где  любая точка, принадлежащая области D.
любая точка, принадлежащая области D.
Пример. Решить задачу Коши: 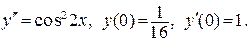
Решение. Найдём сначала 


Итак, получили
 (34)
(34)
Найдем далее у интегрированием уравнения (34):

Получим общее решение:
 (35)
(35)
Найдём константы С 1 и С 2, подставив начальные данные х = 0,  в формулы (34) и (35):
в формулы (34) и (35):



Итак, решение задачи Коши:

 2020-05-12
2020-05-12 757
757








