Определение. Линейным дифференциальным уравнением порядка n называется уравнение вида:
 (36)
(36)
где функции  непрерывны на отрезке
непрерывны на отрезке 
Нетрудно показать, что если  а
а  любые значения, то выполняются все условия теоремы существования и единственности решения задачи Коши для ДУ порядка n.
любые значения, то выполняются все условия теоремы существования и единственности решения задачи Коши для ДУ порядка n.
Рассмотрим ДУ
 (37)
(37)
называемое линейным однородным ДУ, соответствующим неоднородному уравнению (36).
Введём в рассмотрение линейный дифференциальный оператор (ДО):
 (38)
(38)
ДО – это последовательность действий, задаваемая некоторым дифференциальным выражением, в результате которых каждой функции  ставится в соответствие функция
ставится в соответствие функция 
ДО (38) обладает следующими свойствами:
1.  где С – постоянная.
где С – постоянная.
2. 
С помощью ДО (38) однородное уравнение (37) можно записать в виде:
 (39)
(39)
Заметим, что тождественно равная нулю на всём интервале (a, b) функция  является решением однородного уравнения (39).
является решением однородного уравнения (39).
Из свойств ДО возникает важное свойство решений уравнений (39):
если  решения уравнения (39), то их линейная комбинация
решения уравнения (39), то их линейная комбинация  с произвольными коэффициентами С i также является решением этого уравнения.
с произвольными коэффициентами С i также является решением этого уравнения.
Рассмотрим систему функций 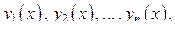 определённых и непрерывных на отрезке
определённых и непрерывных на отрезке 
Определение. Система функций 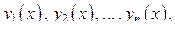 называется линейно зависимой на отрезке
называется линейно зависимой на отрезке  если найдутся такие числа
если найдутся такие числа  одновременно не обращающиеся в нуль, что для всех
одновременно не обращающиеся в нуль, что для всех  имеет место тождество
имеет место тождество  Если же это тождество имеет место лишь тогда, когда все
Если же это тождество имеет место лишь тогда, когда все  то система функций называется линейно независимой на отрезке
то система функций называется линейно независимой на отрезке 
Отметим, что на основании приведённого определения линейная зависимость системы из двух функций  равносильна пропорцио-
равносильна пропорцио-
нальности этих функций, т.е. условию  , где
, где 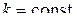
Предположим, что функции  дифференцируемы
дифференцируемы
(n –1) раз на отрезке  и составим определитель:
и составим определитель:
 , (40)
, (40)
называемый определителем Вронского.
Приведём две теоремы об определителе Вронского.
Теорема 1. Если  линейно зависимая на отрезке
линейно зависимая на отрезке 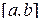 система функций, то определитель Вронского на этом отрезке тождественно равен нулю.
система функций, то определитель Вронского на этом отрезке тождественно равен нулю.
Теорема 2. Если  совокупность n решений ДУ (37) с непрерывными на отрезке
совокупность n решений ДУ (37) с непрерывными на отрезке  коэффициентами
коэффициентами  и эта система функций линейно независима, то определитель Вронского не обращается в нуль ни в одной точке отрезка
и эта система функций линейно независима, то определитель Вронского не обращается в нуль ни в одной точке отрезка 
Следствие. Если определитель Вронского W (x) для системы функций  не принимает значения 0 хотя бы в одной точке отрезка
не принимает значения 0 хотя бы в одной точке отрезка  то эта система функций линейно независимая на
то эта система функций линейно независимая на 
Приведём пример использования определителя Вронского для выяснения вопроса о линейной зависимости или независимости функции на промежутке.
Пример. Доказать, что система функций  где
где  , линейно независима на любом промежутке.
, линейно независима на любом промежутке.
Решение. Найдём определитель Вронского для данной системы функций. Согласно формуле (40) имеем:

Очевидно, что полученный определитель при условии  отличен от нуля при любых значениях х, следовательно, система функций
отличен от нуля при любых значениях х, следовательно, система функций  линейно независима на любом промежутке.
линейно независима на любом промежутке.
Замечание. Аналогично можно показать, что линейно независимой на любом промежутке является и система n функций  , где все
, где все  различны.
различны.
Пример. Доказать, что система функций  где
где  , линейно независима на любом промежутке.
, линейно независима на любом промежутке.
Решение. Найдём определитель Вронского для данной системы функций. Согласно формуле (40) имеем:
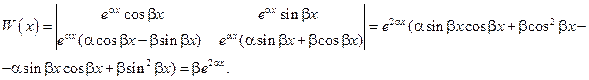
Очевидно, что полученный определитель при условии  отличен от нуля при любых значениях х, следовательно, система функций
отличен от нуля при любых значениях х, следовательно, система функций 
 линейно независима на любом промежутке.
линейно независима на любом промежутке.
Определение. Совокупность n линейно независимых решений ДУ (26) называется фундаментальной системой решений уравнения (26).
Пример. Доказать, что функции 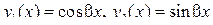 образуют фундаментальную систему решенийуравнения
образуют фундаментальную систему решенийуравнения 


Решение. Вычисляя определитель Вронского для функций 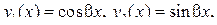 убеждаемся, что он равен
убеждаемся, что он равен  при любом x, и значит, согласно следствию теоремы 1, эти две функции линейно независимы всюду на множестве всех действительных чисел R. (Этот вывод можно сделать также на основании того, что указанные функции непропорциональны друг другу). Кроме того, как нетрудно проверить непосредственно, повторным дифференцированием, каждая из этих функций является решением уравнения
при любом x, и значит, согласно следствию теоремы 1, эти две функции линейно независимы всюду на множестве всех действительных чисел R. (Этот вывод можно сделать также на основании того, что указанные функции непропорциональны друг другу). Кроме того, как нетрудно проверить непосредственно, повторным дифференцированием, каждая из этих функций является решением уравнения  на R. Это и означает, что указанные функции образуют фундаментальную систему решенийданногоуравнения.
на R. Это и означает, что указанные функции образуют фундаментальную систему решенийданногоуравнения.
Теорема (существования фундаментальной системы решений). Для любого однородного ДУ (37) с непрерывными на  коэффициентами существует фундаментальная система решений.
коэффициентами существует фундаментальная система решений.
Доказательство. Пусть  — произвольно фиксированная точка. Построим n решений ДУ (37), удовлетворяющих следующим условиям:
— произвольно фиксированная точка. Построим n решений ДУ (37), удовлетворяющих следующим условиям:

Это возможно в силу теоремы существования и единственности решения задачи Коши для ДУ порядка n.
Очевидно, что в точке  определитель Вронского согласно (40):
определитель Вронского согласно (40):

Поэтому, согласно следствию из теоремы 1, функции  линейно независимы на [ a, b ] и, значит, образуют фундаментальную систему решений ДУ (37).
линейно независимы на [ a, b ] и, значит, образуют фундаментальную систему решений ДУ (37).
Теорема (о структуре общего решения линейного однородного ДУ n -го порядка). Если  фундаментальная система одно-
фундаментальная система одно-
родного ДУ (37), то общее решение этого уравнения имеет вид:
 (41)
(41)
где С1, С2, …, Сn – произвольные постоянные.
3.10. Линейные однородные дифференциальные уравнения
с постоянными коэффициентами. Метод Эйлера
Рассмотрим однородные ДУ (37), в которых коэффициентами  являются постоянные числа
являются постоянные числа  Такие уравнения имеют вид:
Такие уравнения имеют вид:
 (42)
(42)
Будем искать решение уравнения (42) в виде  с некоторым постоянным
с некоторым постоянным  . Тогда
. Тогда 
 Подставляя эти значения в уравнение (42), получаем:
Подставляя эти значения в уравнение (42), получаем:

Поскольку  при любом x, получаем:
при любом x, получаем:
 (43)
(43)
Левая часть равенства (43) называется характеристическим многочленом для уравнения (42) и обозначается:

а его корни называют характеристическими числами. Итак, для того чтобы функция  была решением уравнения (42), необходимо и достаточно чтобы число λ было корнем многочлена
была решением уравнения (42), необходимо и достаточно чтобы число λ было корнем многочлена  т.е. являлось характеристическим числом.
т.е. являлось характеристическим числом.
Задача свелась к нахождению корней алгебраического уравнения (43). Это уравнение степени n, значит, оно, согласно основной теореме алгебры, имеет ровно n (с учётом кратности) действительных или комплексных корней.
Рассмотрим следующие три различных случая, которые могут возникнуть при решении характеристического уравнения.
1. Корни уравнения λ1, λ2, …, λn действительные и различные, им будут соответствовать решения ДУ (42)  Эта система функций линейно независима на всей числовой оси и, следовательно, является фундаментальной системой решений. Тогда, согласно теореме о структуре общего решения линейного однородного ДУ n -го порядка, общее решение ДУ (42) запишется в виде:
Эта система функций линейно независима на всей числовой оси и, следовательно, является фундаментальной системой решений. Тогда, согласно теореме о структуре общего решения линейного однородного ДУ n -го порядка, общее решение ДУ (42) запишется в виде:

2. Среди корней уравнения (43) есть комплексно сопряжённые корни вида  которым будут соответствовать решения
которым будут соответствовать решения 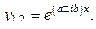 Используя формулу Эйлера
Используя формулу Эйлера  , из них можно построить два действительных линейно независимых решения
, из них можно построить два действительных линейно независимых решения  и
и  которым в общем решении уравнения (42) будут соответствовать слагаемые:
которым в общем решении уравнения (42) будут соответствовать слагаемые:

3. Среди корней уравнения (32) имеется корень λ кратности k. Можно показать, что этому корню в общем решении уравнения (31) будут соответствовать слагаемые:

Пример. Найти общее решение ДУ:
а)  б)
б) 
Решение.
а) 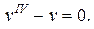 Характеристическое уравнение имеет вид:
Характеристическое уравнение имеет вид:  Оно имеет два различных действительных корня
Оно имеет два различных действительных корня  что соответствует случаю 1 и пару комплексно сопряжённых корней
что соответствует случаю 1 и пару комплексно сопряжённых корней 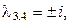 что соответствует случаю 2. Следовательно, общее решение имеет вид:
что соответствует случаю 2. Следовательно, общее решение имеет вид:
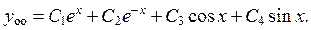
б)  Характеристическое уравнение имеет вид:
Характеристическое уравнение имеет вид:  Оно имеет корни
Оно имеет корни  (корень кратности k =3) и
(корень кратности k =3) и  (корень кратности k =2), что соответствует рассмотренному выше случаю 3. Следовательно, общее решение имеет вид:
(корень кратности k =2), что соответствует рассмотренному выше случаю 3. Следовательно, общее решение имеет вид:

Всё изложенное выше применим к случаю ДУ 2-го порядка, как часто встречающемуся и притом весьма важному.
Линейные однородные ДУ 2-го порядка с постоянными коэффициентами имеют вид:
 (44)
(44)
где р 1 и р 2 — действительные числа.
Согласно теореме о структуре общего решения линейного однородного ДУ достаточно найти два линейно независимых частных решения 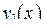 и
и  уравнения (44), чтобы записать общее решение:
уравнения (44), чтобы записать общее решение:

Будем искать решение уравнения (44) по методу Эйлера. Запишем характеристическое уравнение для ДУ (44):
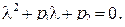 (45)
(45)
Корни  и
и 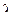 этого квадратного уравнения (с действительными коэффициентам
этого квадратного уравнения (с действительными коэффициентам  и
и  ) могут быть либо действительными, различными или совпадающими, либо комплексно сопряженными. Поэтому согласно сказанному выше, возможны лишь следующие три случая:
) могут быть либо действительными, различными или совпадающими, либо комплексно сопряженными. Поэтому согласно сказанному выше, возможны лишь следующие три случая:
а) Корни  и
и  действительные и различные. Тогда общее решение уравнения (44) имеет вид:
действительные и различные. Тогда общее решение уравнения (44) имеет вид:
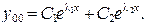 (46)
(46)
б) Корни  и
и  действительные и равные,
действительные и равные,  Общее решение уравнения (44) имеет вид:
Общее решение уравнения (44) имеет вид:
 (47)
(47)
в) Корни  и
и  комплексно сопряженные,
комплексно сопряженные,  Тогда общее решение уравнения (44) имеет вид:
Тогда общее решение уравнения (44) имеет вид:
 (48)
(48)
Пример. Найти общие решения линейных однородных ДУ 2-го порядка с постоянными коэффициентами:
а) 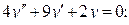 б)
б) 
в)  г)
г) 
Решение.
а) 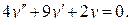 Составим характеристическое уравнение:
Составим характеристическое уравнение:

Решим его, используя известную формулу корней квадратного уравнения:
 (49)
(49)
Получим корни:

Поскольку  R и
R и  то общее решение запишем в виде (46):
то общее решение запишем в виде (46):

б) 
Характеристическое уравнение:

его корни: 
Поскольку  R, то общее решение запишем в виде (47):
R, то общее решение запишем в виде (47):

в) 
Характеристическое уравнение:

его корни: 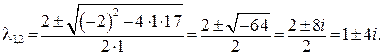
Получили пару комплексно сопряженных корней вида  где а = 1,
где а = 1,
b = 4. Общее решение запишем в виде (48):

г) 
Характеристическое уравнение:

Решим его:

Получили пару комплексно сопряженных корней вида  где а = 0, b = 1,3. Общее решение запишем в виде (48), при этом учтем, что
где а = 0, b = 1,3. Общее решение запишем в виде (48), при этом учтем, что 

3.11. Линейные неоднородные дифференциальные уравнения
высших порядков
Вернёмся к рассмотрению линейных неоднородный ДУ (36). Используя ДО (27), это уравнение можно переписать в виде
 . (50)
. (50)
Отметим некоторые свойства решений уравнения (36), которые вытекают из свойств ДО:
1. Если  решение уравнения (36), а
решение уравнения (36), а  решение соответствующего однородного уравнения L [ y (x)]=0, то
решение соответствующего однородного уравнения L [ y (x)]=0, то  решение неоднородного уравнения (36).
решение неоднородного уравнения (36).
2. Если  и
и  решение уравнения
решение уравнения  , а
, а  решение уравнения
решение уравнения  , то
, то  решение уравнения
решение уравнения  .
.
Это свойство называют принципом суперпозиции решений линейных неоднородных ДУ. Отметим, что этот принцип справедлив для любого конечного числа слагаемых в составе правой части уравнения (50).
Теорема (о структуре общего решения линейного неоднородного ДУ n -го порядка). Если 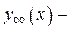 общее решение однородного ДУ (37), а
общее решение однородного ДУ (37), а  какое-либо, произвольное, частное решение неоднородного ДУ (36), то общее решение неоднородного ДУ (36) запишется в виде:
какое-либо, произвольное, частное решение неоднородного ДУ (36), то общее решение неоднородного ДУ (36) запишется в виде:
 (51)
(51)
Следствие. Если  фундаментальная система решений ДУ (37), то общее решение ДУ (36) имеет вид:
фундаментальная система решений ДУ (37), то общее решение ДУ (36) имеет вид:

3.12. Линейные неоднородные дифференциальные уравнения
с постоянными коэффициентами
Рассмотрим неоднородные ДУ (36), в которых коэффициентами  являются постоянные числа
являются постоянные числа  Такие уравнения имеют вид:
Такие уравнения имеют вид:
 (52)
(52)
Из предыдущей теоремы следует, что для решения этого уравнения достаточно найти общее решение соответствующего однородного уравнения и какое-нибудь частное решение данного неоднородного уравнения. В некоторых случаях частное решение отыскивается просто.
Рассмотрим, в каком виде можно искать частное решение  ДУ (36), когда правая часть уравнения
ДУ (36), когда правая часть уравнения  имеет специальный вид.
имеет специальный вид.
Пусть правая часть уравнения имеет вид:
 (53)
(53)
где  многочлены от х степеней n и m соответственно с известными коэффициентами.
многочлены от х степеней n и m соответственно с известными коэффициентами.
Тогда частное решение  следует искать в виде:
следует искать в виде:
 (54)
(54)
где k – кратность корня  характеристического уравнения. Если же числа
характеристического уравнения. Если же числа  не являются корнями характеристического уравнения, то будем считать k =0.
не являются корнями характеристического уравнения, то будем считать k =0.
При этом  многочлены от х степени
многочлены от х степени  с
с
некоторыми, пока неизвестными, коэффициентами. Неизвестные коэффициенты многочленов  и
и  находят методом неопределенных коэффициентов. Поясним суть этого метода следующим примером.
находят методом неопределенных коэффициентов. Поясним суть этого метода следующим примером.
Пример. Найти общее решение линейных неоднородных ДУ 2-го порядка с постоянными коэффициентами:
а)  б)
б) 
Решение.
а) 
Найдём общее решение соответствующего однородного ДУ:

Характеристическое уравнение: 
Поскольку 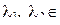 R и
R и  то общее решение запишем в виде (46), при этом учтём, что
то общее решение запишем в виде (46), при этом учтём, что 

Найдём частное решение неоднородного уравнения. Правая часть уравнения  Сравнивая ее с видом (53) заключаем, что
Сравнивая ее с видом (53) заключаем, что  Определим параметры частного решения (54). Учитывая, что
Определим параметры частного решения (54). Учитывая, что  а
а  заключаем, что
заключаем, что  не являются корнями характеристического уравнения, поскольку корни
не являются корнями характеристического уравнения, поскольку корни 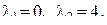 Следовательно, считаем k = 0. Найдём
Следовательно, считаем k = 0. Найдём  Значит, порядок многочленов R и S равен 0, т. е. R 0 = A, а S 0 = B, где А и В – некоторые неизвестные пока коэффициенты. Подставляя полученные параметры в выражение (54), получаем:
Значит, порядок многочленов R и S равен 0, т. е. R 0 = A, а S 0 = B, где А и В – некоторые неизвестные пока коэффициенты. Подставляя полученные параметры в выражение (54), получаем:

Коэффициенты А и В определим из условия, что функция у чн должна быть решением уравнения и поэтому должна ему удовлетворять. Найдем  и
и 

и подставим в исходное уравнение:

Приравняем коэффициенты при  и
и  в правой и левой частях полученного тождества:
в правой и левой частях полученного тождества:


Итак, 
Следовательно, согласно (51) общее решение неоднородного ДУ имеет вид:

б) 
Найдём общее решение соответствующего однородного ДУ:

Характеристическое уравнение:  его корни:
его корни:

Поскольку  R и
R и  то общее решение запишем в виде (46):
то общее решение запишем в виде (46):

Найдём далее частное решение неоднородного уравнения. Правая часть уравнения  Сравнивая её с видом (53), имеем
Сравнивая её с видом (53), имеем  Определим параметры частного решения (54). Учитывая, что
Определим параметры частного решения (54). Учитывая, что 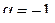 а
а 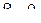 получим, что
получим, что  однократный корень характеристического уравнения, поскольку его корни
однократный корень характеристического уравнения, поскольку его корни  Следовательно, считаем k = 1. Найдем
Следовательно, считаем k = 1. Найдем  Значит, порядок многочленов R и S равен 1, т. е.
Значит, порядок многочленов R и S равен 1, т. е.  а
а  где А, В, С, D – неизвестные коэффициенты. Подставляя полученные параметры в выражение частного решения вида (54), имеем:
где А, В, С, D – неизвестные коэффициенты. Подставляя полученные параметры в выражение частного решения вида (54), имеем:
 Для определения коэффициентов А и В найдём
Для определения коэффициентов А и В найдём  и
и 

и подставим в исходное уравнение:

Поделив обе части уравнения на  и приводя подобные члены, получим тождество:
и приводя подобные члены, получим тождество:

Приравняем коэффициенты при одинаковых степенях х в правой и левой частях полученного тождества:

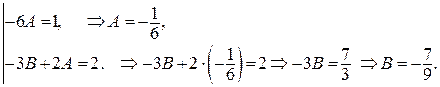
Итак,  и окончательно получаем общее решение неоднородного ДУ:
и окончательно получаем общее решение неоднородного ДУ:

Ряды
 2020-05-12
2020-05-12 545
545