2020-05-12
722
Задача Коши для ДУ 1-го порядка состоит в следующем: из общего решения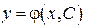 
требуется выделить такое решение 
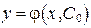уравнения (22), которое удовлетворяет начальному условию: 
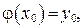где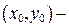 
заданная точка плоскости XOY. Условия существования и единственности решения задачи Коши сформулированы в следующей теореме.
Теорема. Если функция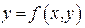 
определена и непрерывна в некоторой области D на плоскости XOY, а частная производная 
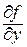ограничена в этой области, то каковы бы ни были числа 
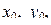такие, что точка 
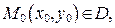найдётся единственная функция 
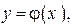являющаяся решением уравнения (22), непрерывно дифференцируемая на некотором промежутке, содержащем точку x 0, и такая, что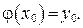 
Пример. Определить тип ДУ и решить задачу Коши
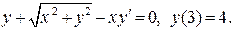
Решение. Для определения типа ДУ выразим из уравнения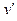 
:
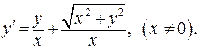
Внесем х под знак корня, возведя его в квадрат:
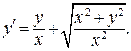
В подкоренном выражении поделим почленно числитель на знаменатель и получим:
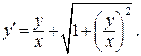(32)
Итак, привели уравнение к виду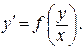 
По таблице ДУ (см. прил. III) определяем, что уравнение однородное и решается заменой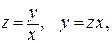 
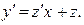Сделаем замену в уравнении (32): 
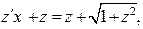учтём, что
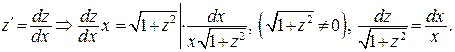
Используя формулы 12 и 4 таблицы интегралов, получаем:
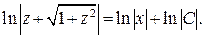
Произвольную постоянную интегрирования выразили в виде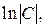 
что позволяет, используя свойства логарифмов, записать общее решение
в виде:
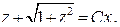
Учитывая выполненную замену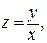 
получаем 
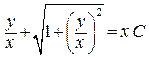– общее решение ДУ в неявном виде, т.е. общий интеграл.
Найдём такое решение, которое удовлетворяет начальному условию у (3) = 4. Для этого подставим в общий интеграл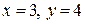 
и найдём значение постоянной С:
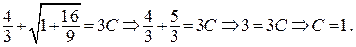
Итак, нашли значение постоянной С, при котором решение ДУ будет удовлетворять указанному начальному условию.
Решение задачи Коши запишем, подставив в общий интеграл найденное значение постоянной С:
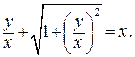
3.6. Ломанные Эйлера и понятие о приближённом методе
решения дифференциальных уравнений
Рассмотрим ДУ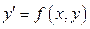 
, и пусть D – область определения функции 
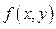, в которой выполнены условия теоремы существования и единственности решения задачи Коши. К одному из способов приближённого решения ДУ приводит геометрическая интерпретация уравнения.
 |
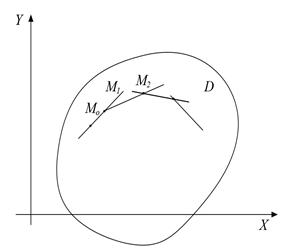| Рис.12 |
А именно, построив поле направлений, мы всегда можем приближённо построить интегральную кривую. Но можно поступить иначе. Пусть точка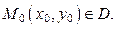 
Проведём через эту точку прямую с угловым коэффициентом, равным 
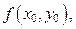и выберем на этой прямой произвольно точку 
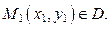Через эту точку М 1 проведём прямую с угловым коэффициентом, равным 
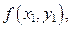и выберем на этой прямой произвольно точку 
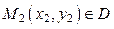и так дальше. Аналогичное построение проведём в другую сторону от точки М 0. В результате получим ломанную линию М 0 М 1 М 2… (рис. 12), каждое звено М k-1 М k которой совпадает с касательной к интегральной кривой в точке М k-1, поэтому эта ломанная (она называется ломанной Эйлера) даёт приближённое представление об интегральной кривой. Это представление тем точнее, чем короче звенья ломанной. Можно показать, что в пределе, при неограниченном увеличении звеньев ломанной и уменьшении длин каждого звена, ломанная Эйлера совпадёт с интегральной кривой.
