2020-05-12
152
Если функция f (x) бесконечно дифференцируема в некоторой окрестности точки х =0, и все ее производные в этой окрестности ограничены одним числом: 
, п = 0,1,2…, то она раскладывается в ряд Маклорена
,
сходящийся в каждой точке этой окрестности к значению функции f (x).
Приведем разложения в ряды Маклорена (степенные ряды) элементарных функций с указанием области сходимости соответствующих рядов.
1) 
.
2) 
,
.
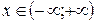3) 
, 
.
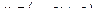4) 
.
5) 
.
6) 
.
7) 
Пример 7. Разложить заданные функции в ряды по степеням 
и указать области сходимости полученных рядов:
а) 
; х 0=0; б)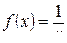 
; х 0=2.
Решение.
а) . Преобразуем заданную функцию: = 
.
Используя разложение
,
, при y= 4 x, найдем:
,
.
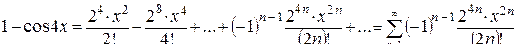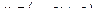Следовательно, 
= 
, окончательно получаем:
= 
, .
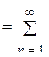
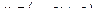б) 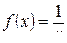; х 0=2. Для того чтобы разложить функцию f (x) в ряд по степеням (х−2), представим ее в виде:
.
Используя разложение
,
при 
, получим:
.
Область сходимости этого ряда определяется неравенством 
, т. е. 
или 0 < х < 4.
Следовательно, 
, и окончательно
получаем:
.
Полученный ряд сходится при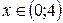 
.
Приближенные вычисления с помощью степенных рядов
С помощью разложения функций в степенные ряды можно вычислять приближенно определенные интегралы от функций, которые не интегрируются аналитически. Известно, что степенной ряд можно почленно интегрировать по любому отрезку строго внутреннему к его промежутку сходимости и почленно дифференцировать в любой внутренней точке его промежутка сходимости любое число раз, при этом радиус сходимости ряда не меняется.
