Дифференциальным уравнением (ДУ) 1-го порядка согласно (21) называется уравнение вида:
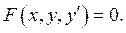
Рассмотрим уравнение, разрешённое относительно производной:
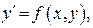 (22)
(22)
связывающее независимую переменную х, неизвестную функцию y = y (x) и её первую производную  . Здесь f (x, y) — некоторая заданная функция своих аргументов, определённая и непрерывная в области D на плоскости XOY. Область D называется областью определения уравнения (ООУ).
. Здесь f (x, y) — некоторая заданная функция своих аргументов, определённая и непрерывная в области D на плоскости XOY. Область D называется областью определения уравнения (ООУ).
Определение. Функция 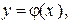 определенная и дифференцируемая на некотором интервале (а, b), называется решением уравнения (22), если, будучи подставленной в это уравнение, она обращает его в тождество, т. е.
определенная и дифференцируемая на некотором интервале (а, b), называется решением уравнения (22), если, будучи подставленной в это уравнение, она обращает его в тождество, т. е. 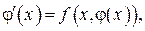 при
при  График решения ДУ называется его интегральной кривой.
График решения ДУ называется его интегральной кривой.
ДУ (22) имеет бесчисленное множество решений вида 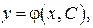 зависящих от одной произвольной постоянной С. Такое решение называется общим решением ДУ. Решение ДУ (22), которое получается из общего решения
зависящих от одной произвольной постоянной С. Такое решение называется общим решением ДУ. Решение ДУ (22), которое получается из общего решения 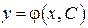 при фиксированном значении С, называется частным решением.
при фиксированном значении С, называется частным решением.
Не всегда решение ДУ (22) находится в виде  иногда оно получается в неявном виде
иногда оно получается в неявном виде 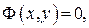 при этом для всех х и y из некоторой области должно выполняться
при этом для всех х и y из некоторой области должно выполняться  Решение
Решение 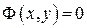 называют интегралом ДУ (22), а уравнение
называют интегралом ДУ (22), а уравнение 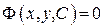 — общим интегралом ДУ (22) в некоторой области
— общим интегралом ДУ (22) в некоторой области 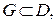 если при надлежащем выборе постоянной С оно даёт любое решение ДУ (22), график которого содержится в области G.
если при надлежащем выборе постоянной С оно даёт любое решение ДУ (22), график которого содержится в области G.
3.3. Геометрическая интерпретация дифференциального
уравнения 1-го порядка и его решения
Рассмотрим ДУ (22). Будем предполагать, что функция 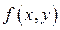 определена в некоторой области D. Возьмём точку
определена в некоторой области D. Возьмём точку  и вычислим
и вычислим  Проведём через точку
Проведём через точку 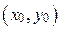 отрезок, например единичной длины, составляющий с осью ОХ угол α, такой, что
отрезок, например единичной длины, составляющий с осью ОХ угол α, такой, что 

|
| Рис.10 |
Рассмотрим другую точку 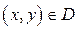 и проделаем то же самое. И так поступим с каждой точкой области D (рис. 10). Таким образом, с каждой
и проделаем то же самое. И так поступим с каждой точкой области D (рис. 10). Таким образом, с каждой
точкой, принадлежащей области D, связано некоторое направление; другими словами говорят, что ДУ (22) определяет некоторое поле направлений.
Пусть 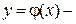 решение ДУ (22), график которого проходит через точку
решение ДУ (22), график которого проходит через точку 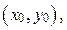 т.е.
т.е.  Кроме того
Кроме того  и, в частности,
и, в частности,
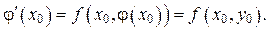 (23)
(23)
В правой части равенства (23) стоит число 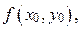 определяющее направление поля в точке
определяющее направление поля в точке 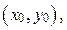 а в левой части – число
а в левой части – число 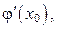 определяющее направление касательной к интегральной кривой в точке
определяющее направление касательной к интегральной кривой в точке 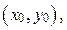 т.е. касательная в каждой точке интегральной кривой имеет то же направление, что и направление поля, создаваемое уравнением (22).
т.е. касательная в каждой точке интегральной кривой имеет то же направление, что и направление поля, создаваемое уравнением (22).
В силу сказанного интегральную кривую можно определить иначе, а именно, интегральная кривая ДУ (22) – это такая кривая, которая в каждой своей точке касается направления поля, создаваемого этим уравнением.
Пример. Построить поле направлений, создаваемое ДУ 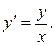
Решение. ООУ – вся плоскость ОХУ, за исключением прямой 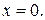 Задача облегчается, если поле направлений строить не в каждой точке, а предварительно найти такие линии, вдоль которых направление поля
Задача облегчается, если поле направлений строить не в каждой точке, а предварительно найти такие линии, вдоль которых направление поля
|
| Рис. 11 |
одинаково. Такие линии называют изоклинами.
Уравнение изоклины для
ДУ (22) 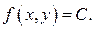 Для нашего примера уравнение изоклины, очевидно, следующее
Для нашего примера уравнение изоклины, очевидно, следующее 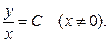 Учитывая, что поле направлений определено всюду, кроме прямой
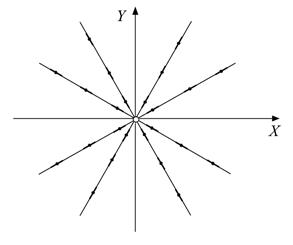
Учитывая, что поле направлений определено всюду, кроме прямой 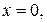 заключаем, что изоклинами являются полупрямые, выходящие из начала координат, не лежащие на оси ординат
заключаем, что изоклинами являются полупрямые, выходящие из начала координат, не лежащие на оси ординат 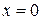 (рис. 11). В каждой точке полупрямой направление поля совпадает с направлением этой полупрямой
(рис. 11). В каждой точке полупрямой направление поля совпадает с направлением этой полупрямой 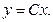 Очевидно, что интегральными прямыми будут полупрямые
Очевидно, что интегральными прямыми будут полупрямые 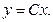
 2020-05-12
2020-05-12 299
299








