Уравнения с разделяющимися переменными

Такие ДУ имеют вид:

(24)

и решаются следующим образом: так как 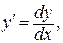то уравнение (24) можно записать в виде 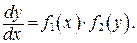Разделим переменные в полученном равенстве, т. е. при дифференциале dy соберем множителями функции, зависящие от y, а при дифференциале dх –функции, зависящие от х. Для этого умножим обе части уравнения (24) на множитель 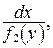считая 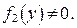Символически это записывается так:

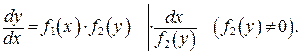
Получим Интегрируя последнее равенство, получим общий интеграл

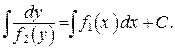
В случае, если уравнение 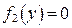имеет решение 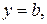то это будет, очевидно, решением исходного ДУ; при этом, если оно
не получается из общего решения или общего интеграла ни при каком значении постоянной С, то такое решение является особым решениемуравнения (24).

Пример. Решить ДУ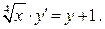

Решение. ДУ приведем к виду (24), разделив обе части равенства на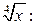

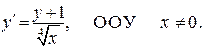
Согласно описанному выше алгоритму, заменив 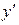на 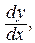получим 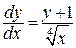и умножим обе части равенства на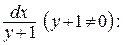

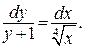(25)

Проинтегрируем полученное равенство:

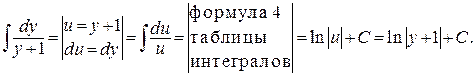
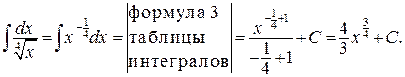
Вернёмся к равенству (25), оставив константу С только в правой части в виде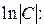

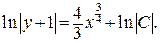
Используя свойства логарифмов, получаем общее решение исходного ДУ: .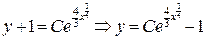

Проверим, имеет ли уравнение особые решения. Уравнение делили на (y + 1), поэтому могли потерять решение y = – 1. Подстановка в уравнение показывает, что y = – 1 решение, однако оно содержится в общем решении при С = 0. Таким образом, особых решений нет.

Однородные уравнения

Однородные ДУ 1-го порядка имеют вид:

(26)

Это уравнение сводится к уравнению с разделяющимися переменными при помощи замены 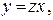где 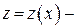новая искомая функция. Действительно, подставляя в уравнение (26) 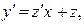получаем: 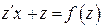— уравнение с разделяющимися переменными. Разделяя переменные, получаем:

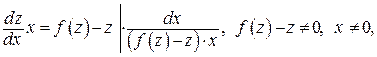
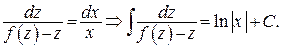
После вычисления интеграла вместо z нужно подставить 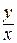и, если можно, упростить полученное выражение.

Пример. Найти общее решение ДУ

Решение. Разделим уравнение на (х = 0 не принадлежит ООУ) и получим: 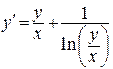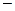однородное уравнение вида (26), в котором

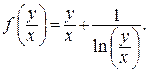
Делаем замену 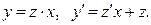Тогда исходное уравнение становится уравнением с разделяющимися переменными:

Найдем интегралы в левой и правой частях полученного равенства:

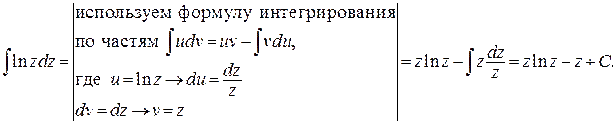
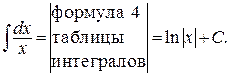
Итак, получаем:

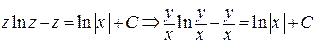
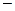общий интеграл исходного ДУ.

Линейные уравнения

Линейные ДУ 1-го порядка имеют вид:

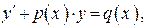(27)

где p (x) и q (x) — известные функции, непрерывные на некотором интервале.

Такие уравнения обычно решают методом Бернулли, который состоит в следующем. Решение ищется в виде произведения двух функций

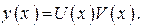Тогда 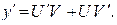Подставляя y и 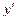в (5), получаем:

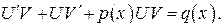
Объединив второе и третье слагаемые в левой части последнего уравнения и вынося U за скобки, и получим:

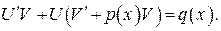(28)

Поскольку одну неизвестную функцию у заменили двумя функциями U и V, то одну из этих функций можем взять произвольно. Выберем функцию V (x) так, чтобы она была решением уравнения

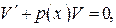(29)

тогда вторая функция U (x) должна удовлетворять уравнению

(30)

Решив уравнение с разделяющимися переменными (29), найдём V и подставим его в (30), откуда найдём U. Общее решение получим как произведение найденных функций U и V:

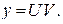
Пример. Найти общее решение ДУ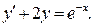

Решение. Уравнение имеет вид (27), поэтому является линейным. Решим его методом Бернулли. Сделаем замену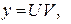

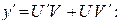
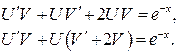
Приравняем коэффициент при U нулю и получим: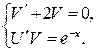

Решим первое из полученных уравнений:

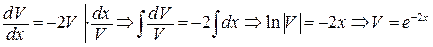(при интегрировании использовали формулы 4 и 2 таблицы интегралов). При нахождении V постоянную С полагаем равной нулю, так как в данном случае достаточно найти некоторое решение.

Полученную функцию 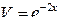подставим во второе уравнение:

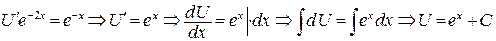(использовали формулы 2 и 7 таблицы интегралов).

Таким образом, 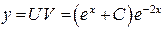или — общее решение исходного ДУ.

Уравнения Бернулли

Уравнения Бернулли имеют вид:

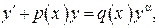(31)

где

Метод решения таких уравнений тот же, что и для линейных уравнений.

Пример. Найти общее решение ДУ

Решение. Разделим уравнение на 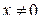(х = 0 не является решением данного ДУ):

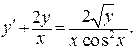
Полученное уравнение имеет вид (31), следовательно, это уравнение Бернулли. Сделаем замену 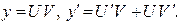Получим:

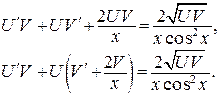
Приравняем коэффициент при U нулю и получим систему уравнений: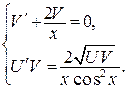

Решим первое уравнение:

(использовали формулу 4 таблицы интегралов).

Подставим полученную функцию V во второе уравнение:

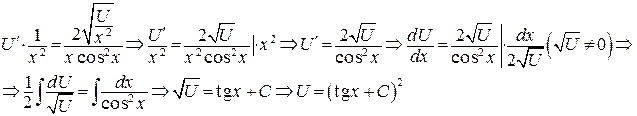(использовали формулы 3 а и 9 таблицы интегралов).

Таким образом, общее решение ДУ:

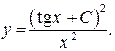
Рассмотрим теперь случаи и V = 0, опущенные выше при решении уравнений системы (поскольку выполнялись деления на V и 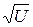). В каждом из этих случаев имеем y = 0, что является решением исходного ДУ, и так как это решение не может быть получено из общего решения, то оно является особым решением.