Драчева И.А., Ершова Т.Г.
МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Часть
Практикум
по самостоятельной работе и выполнению контрольной работы
для студентов направления подготовки 38.03.01 «Экономика»
заочной формы обучения
Керчь, 2016 г.

СОДЕРЖАНИЕ
| ВВЕДЕНИЕ…………………………………………………………………… | 4 |
| ТАБЛИЦА ВЫБОРА ВАРИАНТА ЗАДАНИЙ.…………………………… | 5 |
| ЗАДАНИЯ К КОНТРОЛЬНОЙ РАБОТЕ………………………………. | 5 |
| РЕКОМЕНДАЦИИ ПО ИЗУЧЕНИЮ ТЕОРЕТИЧЕСКИХ ВОПРОСОВ И ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ..……………………………... | 7 |
| 1 Определенный интеграл. Площадь криволинейной трапеции. Задание 1-10……………………………………………………………………………. | 7 |
| 2 Несобственные интегралы. Задание 11-20. ……………………..………. | 9 |
| 3 Дифференциальные уравнения первого порядка. Задание типа 21-30…. | 11 |
| 4 Дифференциальные уравнения второго порядка. Задание типа 31-40…. | 13 |
| 5. Ряды Тейлора. Задание 41-50……………………………………………… | 17 |
| 6 Функция нескольких переменных. Задание типа 51-60………….……… | 20 |
| ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ЭКЗАМЕНУ………………………... | 22 |
| СПИСОК ИСПОЛЬЗОВАННОЙ И РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ | 23 |
ВВЕДЕНИЕ
Цель преподавания математики для студентов экономических направлений ознакомить студентов с основами математического аппарата, необходимого для решения теоретических и практических задач экономики; развить их логическое мышление; привить студентам навыки самостоятельного изучения литературы по математике; повысить общий уровень математической культуры.
Основной формой обучения студента-заочника является самостоятельная работа над учебным материалом по математическим дисциплинам. Она складывается из чтения учебников, методических пособий, решения задач, выполнения контрольных заданий.
Настоящее пособие содержит вопросы для подготовки к экзамену (зачету) по математическому анализу, контрольные задания и методические указания к решению задач за 2 семестр.
При выполнении контрольных работ студент должен следовать следующим рекомендациям:
- Каждую работу необходимо выполнять в отдельной тетради, на обложке которой должны быть указаны номер контрольной работы, фамилия и инициалы студента, полный шифр, дата отсылки работы в университет.
- При решении задач необходимо указать номер задачи и ее содержание. Решение задачи должно сопровождаться достаточно подробными пояснениями.
- Все вычисления должны быть приведены полностью, чертежи и графики выполнены аккуратно.
- Для удобства рецензирования преподавателем контрольной работы следует на каждой странице оставлять поля.
После получения из университета отрецензированной работы студент должен исправить в ней все ошибки. Если работа не допущена к защите, то в кратчайший срок студенту необходимо после устранения замечаний преподавателя представить работу на повторное рецензирование. Ошибки следует исправлять в той же тетради.
Перед экзаменом или зачетом студент должен защитить контрольную работу. Защита предполагает проверку того, что работа выполнена студентом самостоятельно. Поэтому при защите студент должен быть готов дать пояснения к решенным задачам или решить подобные задачи.
На экзамен (или зачет) необходимо представить преподавателю все запланированные контрольные работы.
Студент выполняет во втором семестре по математическому анализу одну контрольную работу, вариант контрольной работы совпадет с последней цифрой его учебного шифра.
ТАБЛИЦА ВЫБОРА ВАРИАНТА ЗАДАНИЙ
| Вариант | Номера задач контрольных заданий | Вариант | Номера задач контрольных заданий | ||||||||
| 1 | 1 | 11 | 21 | 31 | 41 | 6 | 6 | 16 | 26 | 36 | 46 |
| 2 | 2 | 12 | 22 | 32 | 42 | 7 | 7 | 17 | 27 | 37 | 47 |
| 3 | 3 | 13 | 23 | 33 | 43 | 8 | 8 | 18 | 28 | 38 | 48 |
| 4 | 4 | 14 | 24 | 34 | 44 | 9 | 9 | 19 | 29 | 39 | 49 |
| 5 | 5 | 15 | 25 | 35 | 45 | 10 | 10 | 20 | 30 | 40 | 50 |
ЗАДАНИЯ К КОНТРОЛЬНОЙ РАБОТЕ
1-10. Сделать чертеж и вычислить площадь плоской фигуры, ограниченной линиями.
| 1. | у = 0 у = – х 2 + 2 х |
| 2. | х 2 – 4 у = 0; у = 0; х – 6 = 0 |
| 3. | х 2 – 2 у = 0; у – 2 х = 0 |
| 4. | х 3 – 2 у = 0; х – 2 = 0; у = 0 |
| 5. | у + х 2 = 0; х + у = 0 |
| 6. | ху – 2 = 0; у = 0; х – 1 = 0; х – 3 = 0 |
| 7. | 
|
| 8. | 3 у – х 2 = 0; х – у = 0 |
| 9. | ху = 4; х = 1; х = 2; у = 0 |
| 10. | у = х 2; у = 4 |
11-20. Вычислить несобственные интегралы или доказать их расходимость.
11. 
| 12. 
| 13. 
| 14. 
| 15. 
|
16. 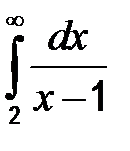
| 17. 
| 18. 
| 19. 
| 20. 
|
21-30. Решить дифференциальное уравнение первого порядка, в случае б) найти частное решение дифференциального уравнения при заданных начальных условиях y (х 0 ) = у 0.
| 21. | а)  ; ;
| б)  ; ;
| х0 =0; | у0= 3. |
| 22. | а)  ; ;
| б)  ; ;
| х0= 0; | у0=  . .
|
| 23. | а)  ; ;
| б)  ; ;
| х0= 0; | у0= 4 |
| 24. | а)  ; ;
| б)  ; ;
| х0= 0; | у0= 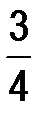
|
| 25. | а)  ; ;
| б)  ; ;
| х0=  ; ;
| у0= 3 |
| 26. | а)  ; ;
| б)  ; ;
| х0= 0; | у0= 5 |
| 27. | а)  ; ;
| б)  ; ;
| х0= 0; | у0= 2. |
| 28. | а) 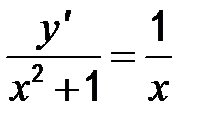 ; ;
| б)  ; ;
| х0= 2; | у0= 5. |
| 29. | а)  ; ;
| б)  ; ;
| х0= 1; | у0= 2. |
| 30. | а)  ; ;
| б)  ; ;
| х0= 3; | у0= 1. |
31-40. Решить неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами и специальной правой частью.
| 31. | 
| 32. | 
|
| 33. | 
| 34. | 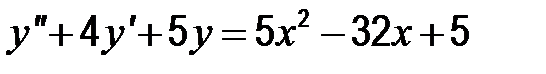
|
| 35. | 
| 36. | 
|
| 37. | 
| 38. | 
|
| 39. | 
| 40. | 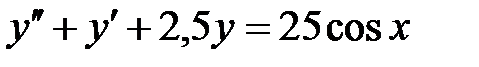
|
41-50. Вычислить определенный интеграл, разложив подынтегральную функцию в ряд.
41. Вычислить с точностью 0,00001 
42. Вычислить с точностью 0,0001 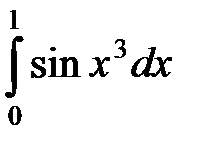
43. Вычислить с точностью 0,0001 
44. Вычислить с точностью 0,0001 
45. Вычислить с точностью 0,0001 
46. Вычислить с точностью 0,0001 
47. Вычислить с точностью 0,0001 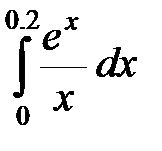
48. Вычислить с точностью 0,001 
49. Вычислить с точностью 0,001 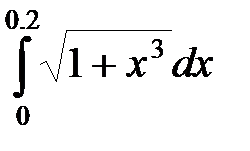
50. Вычислить с точностью 0,001 
51-60. Дана функция z=f (x, y), точка А (х 0, у 0). Требуется найти  в точке А.
в точке А.
| 51. |  ; А (-1; 2) ; А (-1; 2)
| 56. | 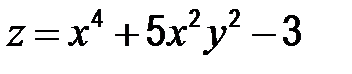 ; А (2; -2) ; А (2; -2)
|
| 52. |  ; А (1; 3) ; А (1; 3)
| 57. | 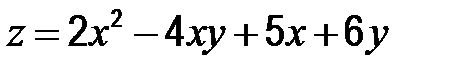 ; А (3;–2) ; А (3;–2)
|
| 53. |  ; А (2; 1) ; А (2; 1)
| 58. | 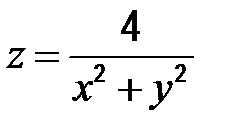 ; А (-2; 2) ; А (-2; 2)
|
| 54. |  ; А (5; 3) ; А (5; 3)
| 59. |  ; А (1; 2) ; А (1; 2)
|
| 55. |  ; А (1; 1) ; А (1; 1)
| 60. |  ; А (1; -2) ; А (1; -2)
|
РЕКОМЕНДАЦИИ ПО ИЗУЧЕНИЮ ТЕОРЕТИЧЕСКИХ ВОПРОСОВ И ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ
Определенный интеграл. Площадь криволинейной трапеции. Задание 1-10.
Пусть функция f (x) определена на отрезке [ а; b ]. Разобьем этот отрезок на n частей произвольным образом точками х 0 = а < x 1 < x 2 < …< x n = b.
Пусть 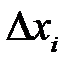 – длина i -го частичного отрезка. На каждом элементарном отрезке
– длина i -го частичного отрезка. На каждом элементарном отрезке  выберем произвольную точку сi, вычислим значение функции в этой точке f (сi), умножим это значение на длину частичного отрезка f (сi)
выберем произвольную точку сi, вычислим значение функции в этой точке f (сi), умножим это значение на длину частичного отрезка f (сi)  . Сложив полученные произведения, получим сумму, которая называется интегральной
. Сложив полученные произведения, получим сумму, которая называется интегральной

Определение:Определенным интегралом от функции f(x) на отрезке [а; b] называется предел последовательности интегральных сумм при условии, что длина наибольшего из частичных отрезков  стремится к нулю, этот предел существует и не зависит от разбиения [а; b] на части и от выбора сi в них:
стремится к нулю, этот предел существует и не зависит от разбиения [а; b] на части и от выбора сi в них:
 Если f (x) ≥ 0 на отрезке [ а; b ], то определенный интеграл
Если f (x) ≥ 0 на отрезке [ а; b ], то определенный интеграл  численно равен площади криволинейной трапеции, т.е. фигуры, ограниченной линией
у = f (x), осью ОХ и прямыми численно равен площади криволинейной трапеции, т.е. фигуры, ограниченной линией
у = f (x), осью ОХ и прямыми  и и  (рис. 1). (рис. 1).
| 
|
 2020-05-12
2020-05-12 124
124







