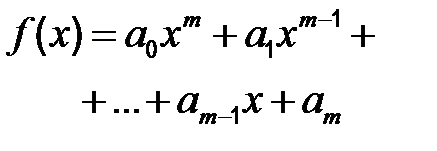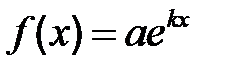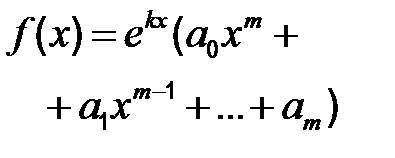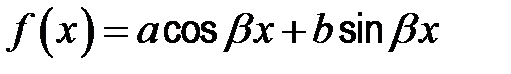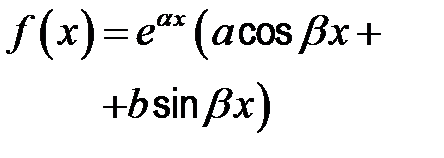2020-05-12
103
Это уравнение имеет вид: y'' + рy' + qу = f (x). Его общее решение записывается в виде суммы функций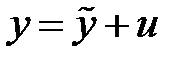 
, где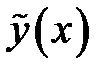 
- общее решение соответствующего однородного уравнения; u (х) – частное решение неоднородного уравнения. Функция u (х) зависит от вида правой части уравнения и может быть найдена по таблице 2.
Таблица 2
| Если правая часть уравнения имеет вид | Частное решение имеет вид | Указание | |||
| 1 |
| 1)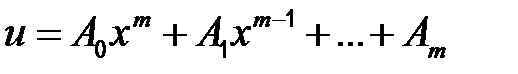 
| Если 0 не корень характеристического уравнения | ||
2) 
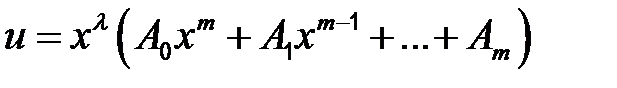
| Если 0 корень характеристического уравнения кратности λ | ||||
| 2 |
| 
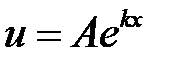
| Если k – не корень характеристического уравнения | ||
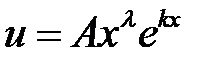
| Если k – корень характеристического уравнения кратности λ. | ||||
| 3 |
| 1)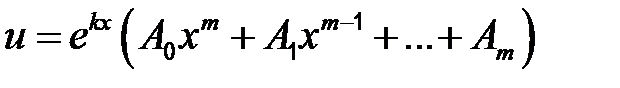 
| Если k – не корень характеристического уравнения | ||
2) 
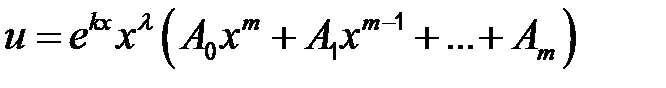
| Если k – является корнем характеристического уравнения кратности λ. | ||||
| 4 |
| 
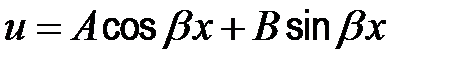
| Если βi – не является корнем характеристического уравнения | ||
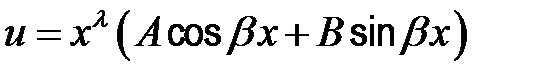
| Если βi – является корнем характеристического уравнения кратности λ. | ||||
| 5
|
| 
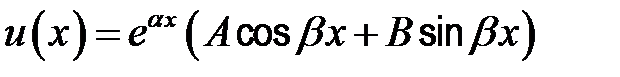
| Если (α+ β i) – не является корнем характеристического уравнения. | ||
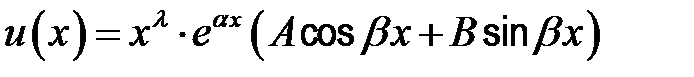
| Если (α+βi) – является корнем характеристического уравнения кратности λ. |
Определение коэффициентов A, B, А 0, А 1, А 2… А m рассмотрим на примерах.
Примеры:
1) y'' – 7 y' +10 у = 2 е 5 х
Составим характеристическое уравнение и решим его:
k 2 – 7 k + 12 = 0;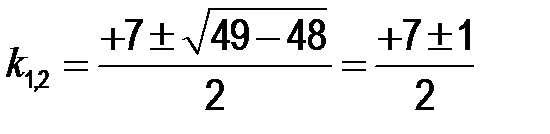 
; k 1 = 3; k 2 = 4. Тогда 
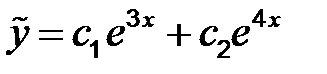. Частное решение согласно таблицы 2 имеет вид: 
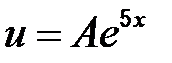(случай 2, табл. 2).
Найдем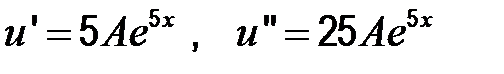 
, подставим 
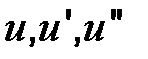вместо 
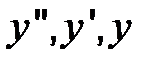в исходное уравнение. Так как u (х) – есть решение нашего уравнения, то
25 Ае 5 х – 75 Ае 5 х + 12 Ае 5 х = 2 е 5 х .
Находим А: 25 А - 35 А + 12 А = 2; 2 А = 2; А = 1. Следовательно,
.
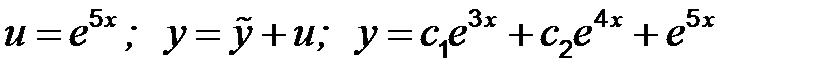2) y'' - 7 y' +6 у = 2 sin x.
Составим характеристическое уравнение и решим его:
; 
;
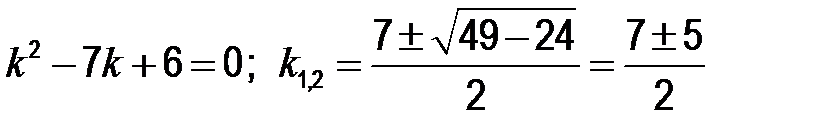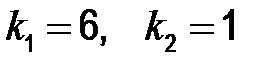Тогда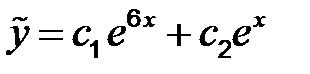 
. Частное решение имеет вид:
u = Аcos x + B sin x (случай 4, табл. 2); u' = - А sin x + B cos x; u'' = - A cos x – B sin x.
Подставим в исходное уравнение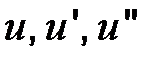 
:
– A cos x – B sin x – 7(– A sin x + B cos x) + 6(A cos x + B sin x) = 2 sin x;
– A cos x – B sin x + 7 А sin x – 7 В сos x + 6 A cos x + 6 B sin x = 2 sin x.
Приравняем коэффициенты при sin x и cos x слева и справа:
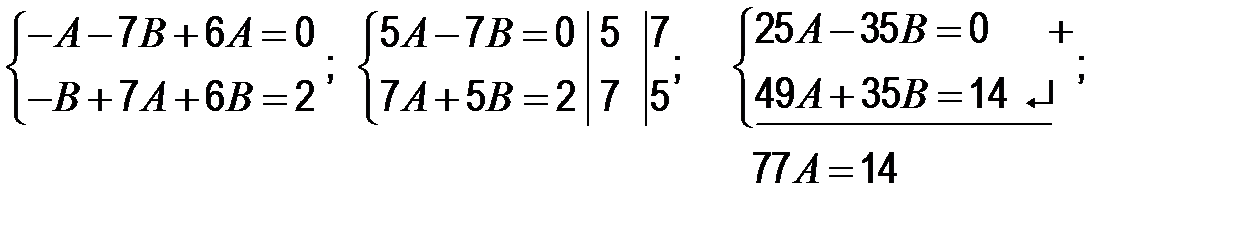
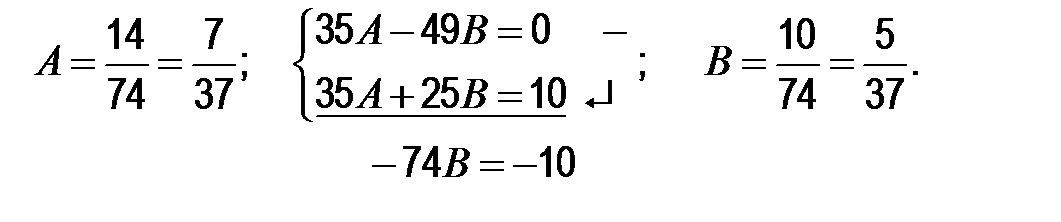
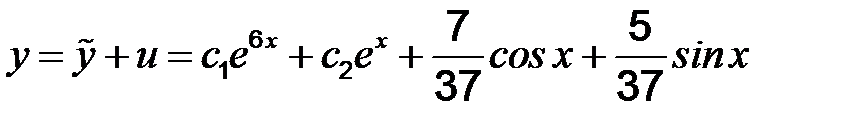
3) 
.
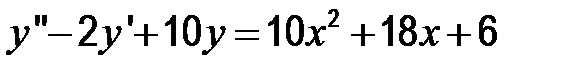Составим характеристическое уравнение:
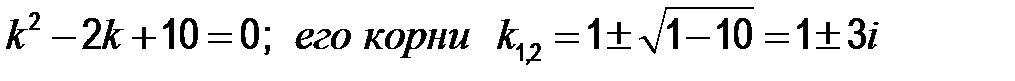
Согласно табл. 1, α = 1; β = 3.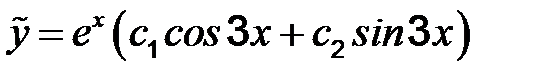 
.
u = Ax 2+ Bx + C (cлучай 1, табл.2). u' = 2 Ax + B; u'' = 2 A.
Подставим в исходное уравнение:
2 А – 2(2 Ах + В) + 10(Ах 2 + Вх + С) = 10 х 2 + 18 х + 6;
2 А – 4 Ах – 2 В + 10 Ах2 + 10 Вх + 10 С = 10 х 2 + 18 х + С;
Приравняем коэффициенты при одинаковых степенях х слева и справа:
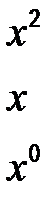
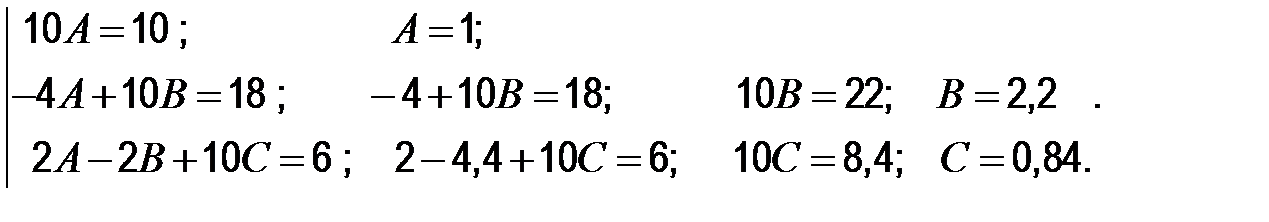
u = x 2 + 2,2 x + 0,84;
.
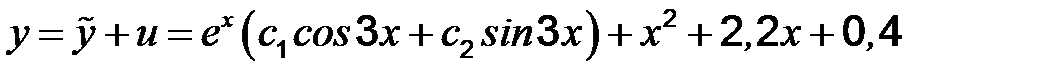4) Найти общее решение дифференциального уравнения и выделить частное решение, удовлетворяющее заданным начальным условиям.
, 
.
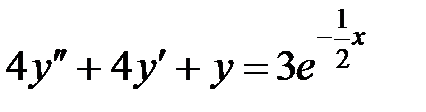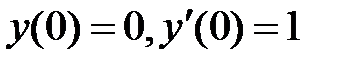а) Составляем характеристическое уравнение
, 
, 
.
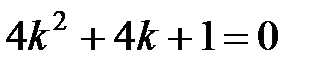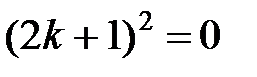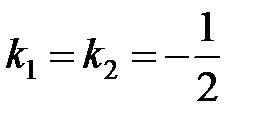Уравнение имеет два одинаковых корня, следовательно, общее решение соответствующего однородного уравнения будет иметь вид
|
|
|
.
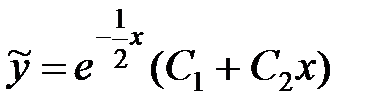б) Правая часть имеет вид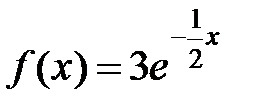 
, где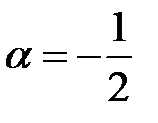 
является двукратным корнем характеристического уравнения (случай 2, λ=2). Частное решение будем искать в виде 
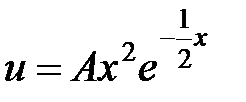. Для определения коэффициента А найдем производные:
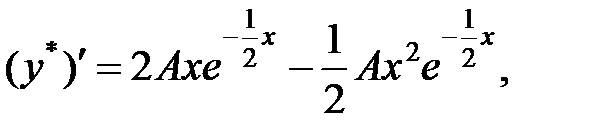
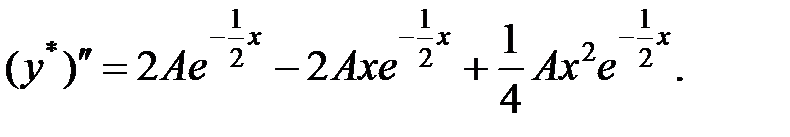
Подставим производные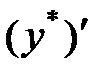 
, 
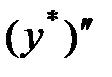и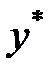 
в исходное уравнение, получим:
;
; 
; 
.
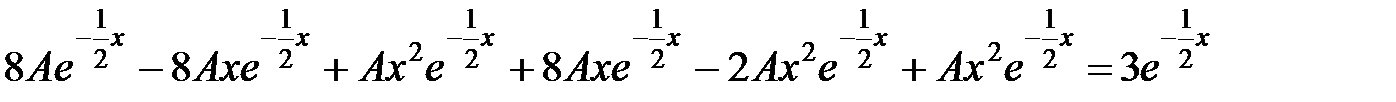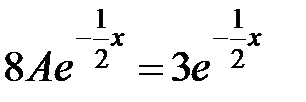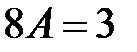Записываем частное решение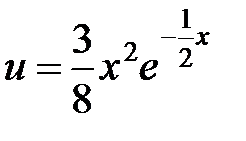 
.
Общее решение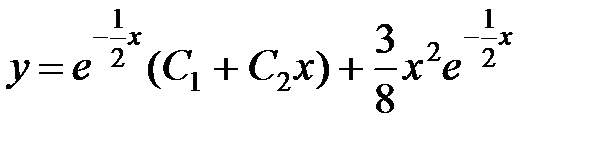 
.
в) Находим частное решение, удовлетворяющее заданным начальным условиям.
Найдем производную:
.
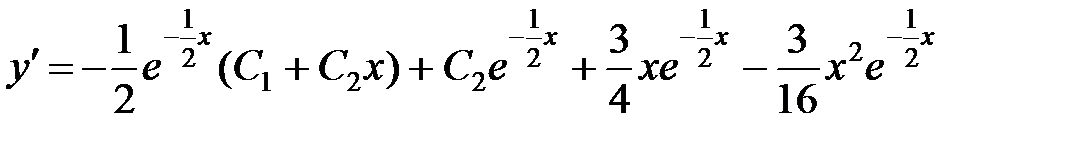Подставим заданные условия 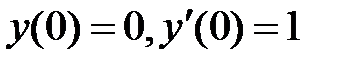в общее решение и производную, получим систему для коэффициентов С1 и С2:
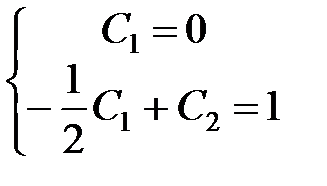. Отсюда 
.
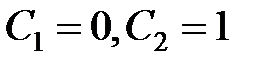Частное решение, удовлетворяющее заданным начальным условиям:
.
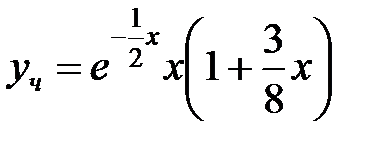Вопросы для самоконтроля.
1. Дайте определение дифференциального уравнения второго порядка.
2. Что называется общим решением дифференциального уравнения второго порядка?
3. Какое уравнение называется линейным уравнением второго порядка с постоянными коэффициентами?
4. Какие уравнения называются однородными и неоднородными?
5. Как составляется характеристическое уравнение?
6. Расскажите алгоритм решения ЛНДУ 2-го порядка с постоянными коэффициентами.
Литература: [4] стр. 344-354, [9] стр. 59-79.
Примеры: [2] стр.145-159; [7] стр.227-228.
