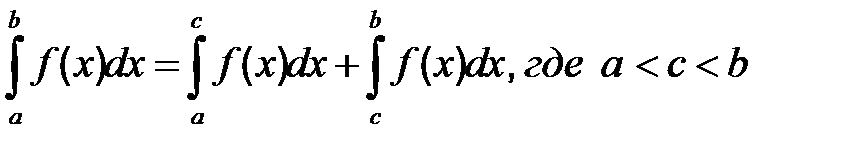2020-05-12
85
1. 
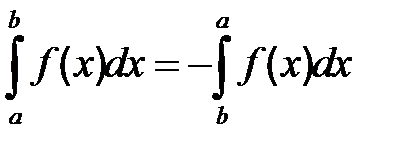
| 2. 
|
| 3. | |
4.  А = const
| 5. 
|
Вычисление определенного интеграла
Формула Ньютона – Лейбница
Определенный интеграл от непрерывной функции f (x) равен разности значений ее первообразной F (x) при х = b и х = а, где а и b нижний и верхний пределы интегрирования, т.е. имеет место формула
где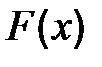 
- одна из первообразных функции f (x).
Пример: 
Вычисление площади плоской фигуры
Если на отрезке [ а; b ] функция f (x) ≥ 0, то согласно геометрическому смыслу определенного интеграла площадь криволинейной трапеции, ограниченной кривой у = f (x), осью ОХ и прямыми х = а и х = b, определяется по формуле
Пример: Вычислить площадь фигуры, ограниченной линиями у = х 2 + 1; у = 0; х = 0; х = 3. Построим фигуру, площадь которой надо найти. Графиком функции у = х 2 + 1 является парабола, симметричная относительно оси ОУ с вершиной в точке В (0; 1) (рис. 2).
Тогда:
| 
|
Если фигура ограничена линиями у = f 1(x) и у = f 2(x), где f 2(x) ≥ f 1(x), и прямыми х =а и х= b, то ее площадь определяется по формуле
Пример: Найти площадь фигуры, ограниченной линиями: у = – х 2 +6 х –5, у = 1 – х.
|
|
|
Построим данную фигуру. Графиком первой функции является парабола,
симметричная относительно прямой, параллельной оси ОУ; ветвь параболы направлена вниз (рис.3).
Найдем точки пересечения параболы с осью ОХ:
– х 2 + 6 х – 5 = 0; х 2 - 6 х + 5 = 0; 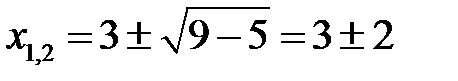 ; х 1 = 5; х 2 = 1.
Найдем точки пересечения параболы с ОУ:
при х = 0 у = – 5.
Построим прямую у = 1 – х:
при х = 0 у = 1; при у = 0 х = 1.
Найдем точки пересечения параболы и прямой:
| 
Рис. 3
|
Решим уравнение: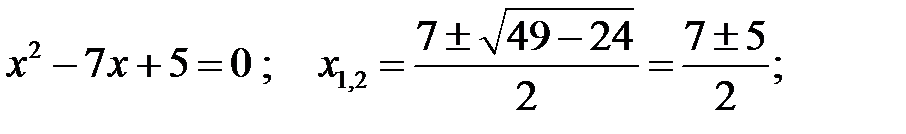 
х 1 = 6; х 2 = 1.
Тогда у 1 = – 5; у 2 = 0. Точки пересечения А (1: 0); В (6; -5)
Вопросы для самоконтроля.
1. Какая фигура называется криволинейной трапецией?
2. Какая задача привела к возникновению интегрального исчисления?
3. Назовите свойства определенного интеграла.
4. Напишите формулу Ньютона-Лейбница.
5. Расскажите, как вычисляется площадь плоской фигуры с помощью интеграла.
Литература: [4] стр. 259-279, [8] стр. 380-401, 429, [6] стр. 298-329.
Примеры: [1] стр. 243-251, [7] стр. 167-170.
