Ряды Тейлора. Задание 41-50

Наиболее простой функцией среди элементарных является многочлен. Он легко дифференцируется и интегрируется. Значения многочлена вычисляются так же значительно легче, чем других функций. В связи с этим встает вопрос, нельзя ли другие, более сложные функции заменить многочленами, не допуская при этом больших погрешностей. Этот вопрос положительно решен по отношению к некоторым функциям с помощью, так называемой формулы Тейлора.

Всякая функция 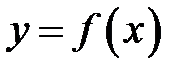 бесконечное число раз дифференцируемая в точке  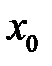и в некоторой ее окрестности 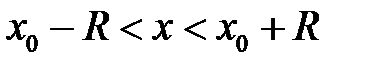, может быть разложена в указанном интервале в сходящийся к ней степенной ряд Тейлора

,

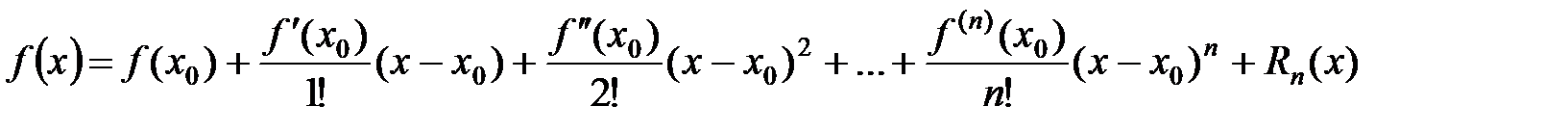если в этом интервале остаток ряда стремится к нулю .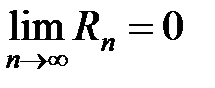

При 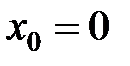 получим ряд Маклорена   

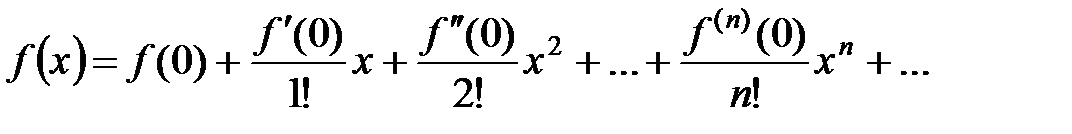
Таблица разложения в ряд Маклорена некоторых элементарных функций.

1)  .

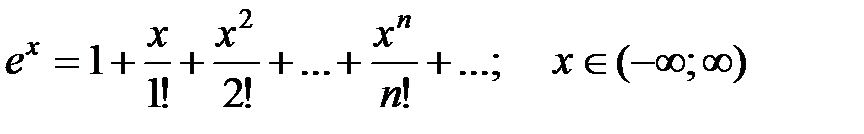2) .

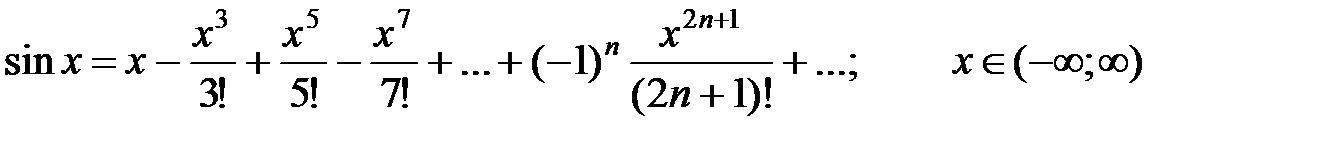3) .

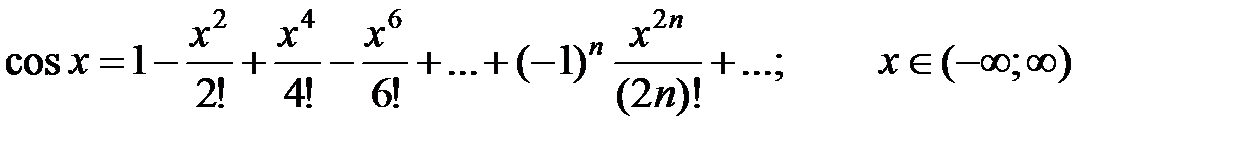4) биноминальный ряд

;

 

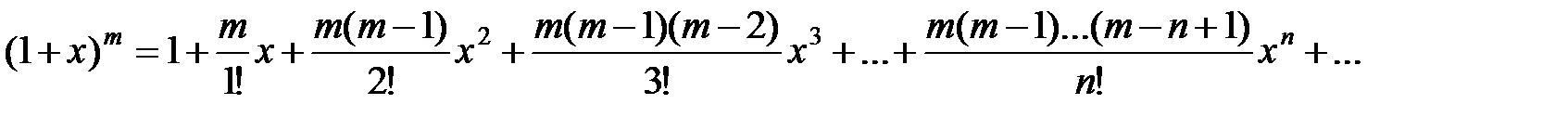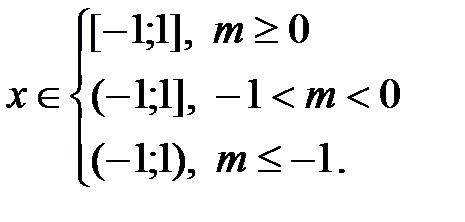
5) .

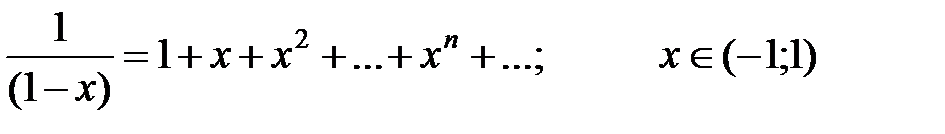6) .

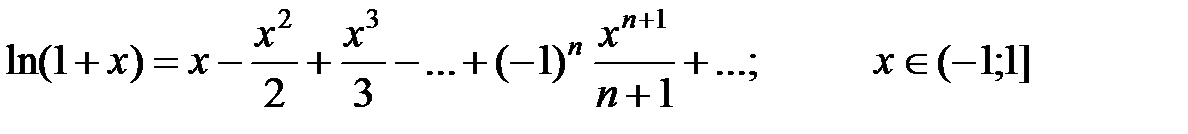7) .

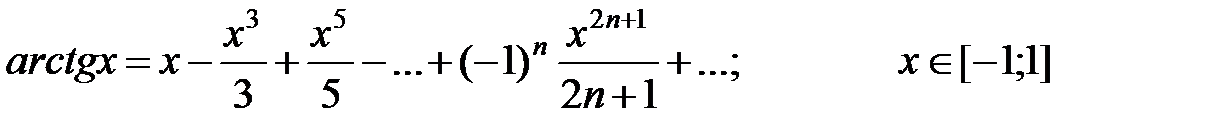8)

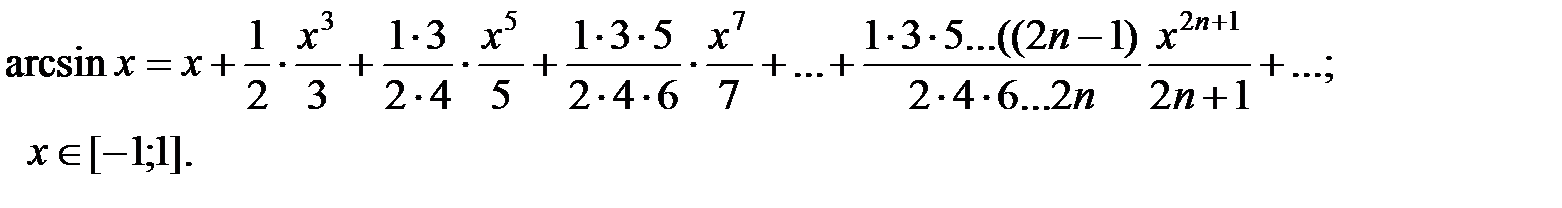
Примеры.

1) Пользуясь таблицей получить разложение для функции 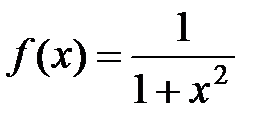. Воспользуемся биноминальным рядом

.

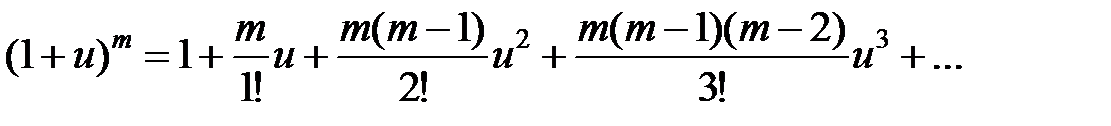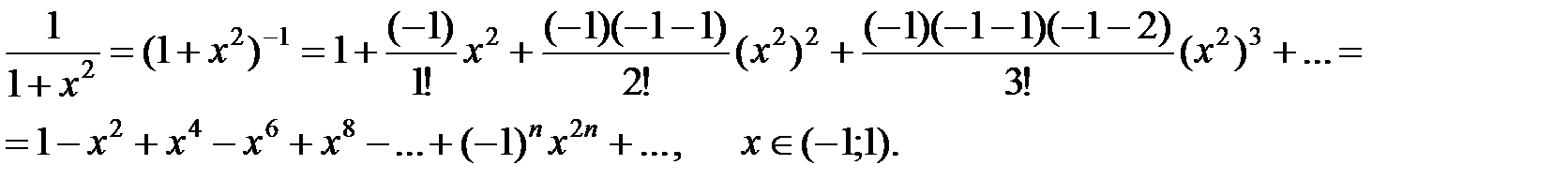
2) Написать ряд Маклорена для функции .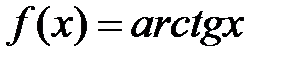

Воспользовавшись свойством степенных рядов [7, с.462], проинтегрируем ряд для функции 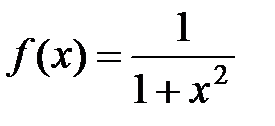, получим:

                     

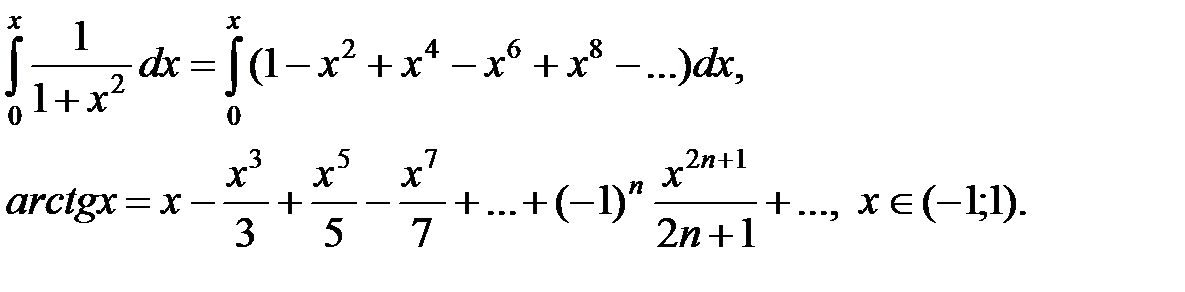
Можно показать, что ряд сходится пр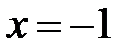и   и .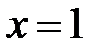

При 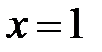,  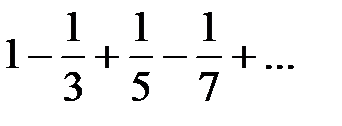 - лейбницевский ряд, сходится.

При 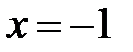,  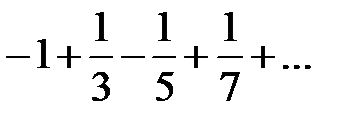- лейбницевский ряд, сходится.

Таким образом, ряд  для  функции 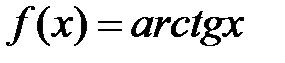 сходится для всех .

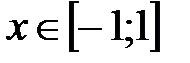Некоторые приложения степенных рядов

1) Ряды Тейлора используются для приближенного вычисления значений функции.

Найти 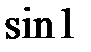    с точностью 0,001.

Разложение функции .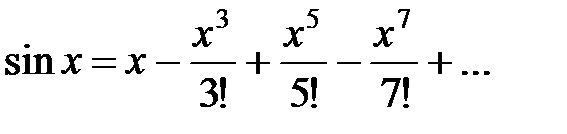

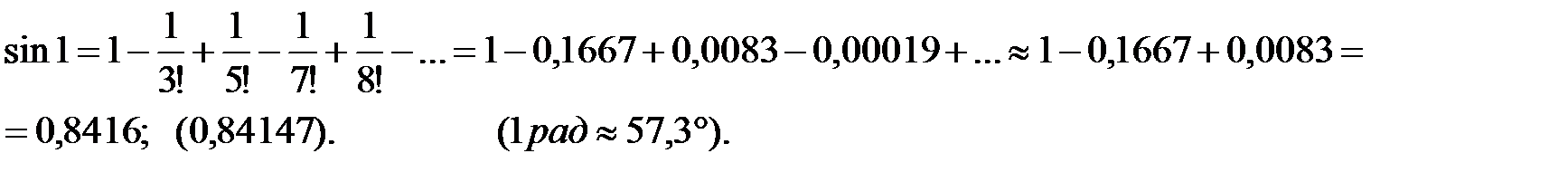
2) Бесконечные ряды применяются также для приближенного вычисления неопределенных и определенных интегралов в случаях, когда первообразная не выражается в конечном виде через элементарные функции, либо нахождение первообразной сложно.

Пусть требуется вычислить 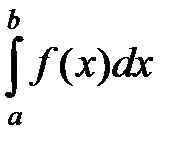 с точностью до 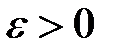. Если подынтегральную функцию  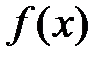можно разложить в ряд по степеням х и интервал сходимости  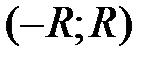включает в себя отрезок 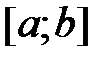, то для вычисления заданного интеграла нужно воспользоваться свойством почленного интегрирования этого ряда.

Пример 1.  Вычислить интеграл 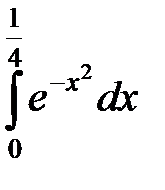 с точностью .

 .

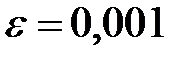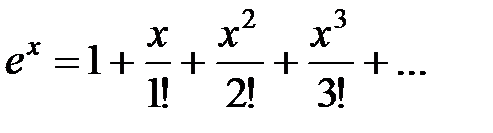Вместо 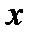 подставим 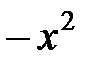, получим: .

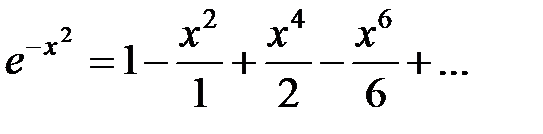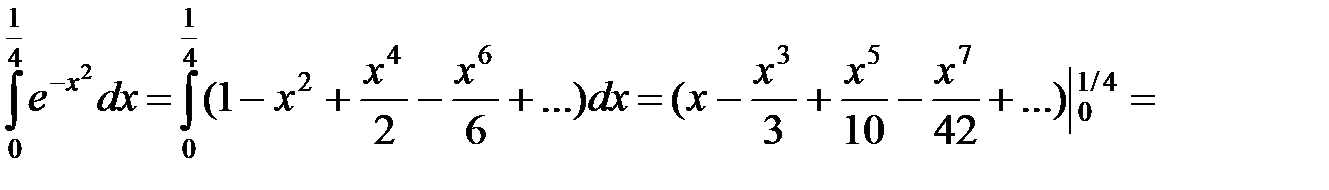
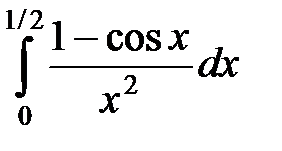Пример 2. Вычислить с точностью 0,0001.

Разложим подынтегральную функцию в степенной ряд, заменив 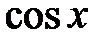  его разложением в ряд Маклорена, получим

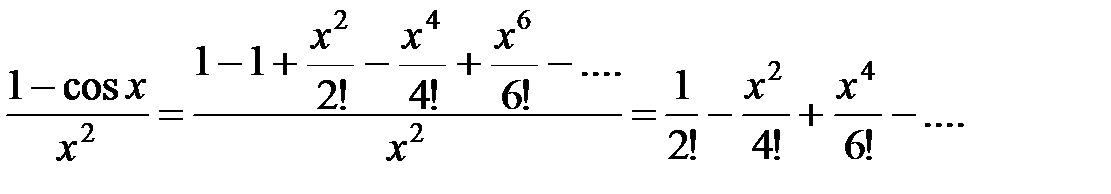
Запишем под знак интеграла вместо подынтегральной функции ее разложение в степенной ряд:

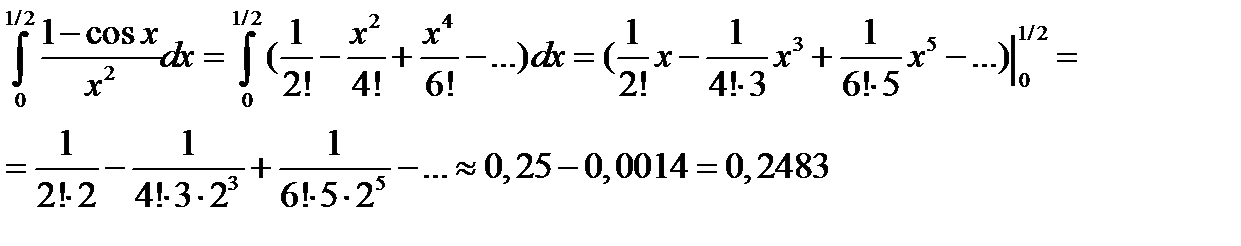
Для вычисления интеграла с точностью 0,0001 можно отбросить все члены, начиная с того, который меньше 0,0001. Третий член разложения меньше 0,0001, поэтому для вычисления интеграла с указанной точностью достаточно взять два слагаемых.

Вопросы для самоконтроля.

1. Напишите формулу разложения функции в ряд Тейлора, Маклорена.

2. Приведите разложение элементарных функций в ряд Маклорена.

3. Где используются степенные ряды?

4. Расскажите последовательность действий при вычислении интеграла с помощью ряда Маклорена.

Литература: [4] стр. 457-473, [8] стр. 143-149, [6] стр. 351-397.

Примеры: [1] стр.81-95, [7] стр. 256-258.

6.  Функция нескольких переменных. Задание 51-60

 

Если каждой паре (х, у) значений двух независимых переменных величин х, у из некоторой области D соответствует определенное значение величины z, то мы говорим, что z есть функция двух независимых переменных, определенная в области D, и пишем z = f (x, y)

Частной производной от функции z = f (x, y) по независимой переменной х называется производная 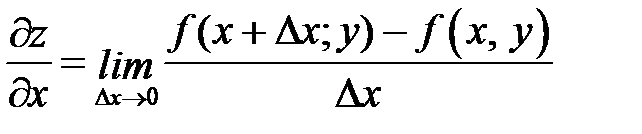, вычисляемая в предположении, что у – постоянная.

Частной производной от функции z = f (x, y) по независимой переменной у называется производная 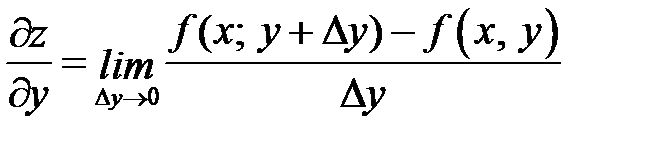, вычисленная в предположении, что х – постоянная.

Градиентом функции z = f (x, y)называется вектор, координатами которого являются частные производные функции z:

.

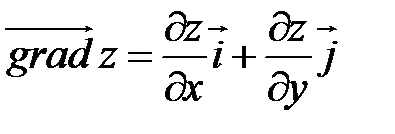В направлении вектора 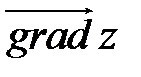 функция изменяется наиболее быстро.

Пример: Даны функция z = x ³ + 2 y ³ – x y и точка А (1; 2). Найти 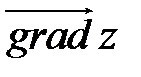 в точке А.

Найдем частные производные ; .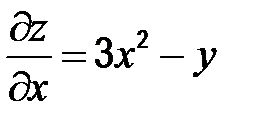

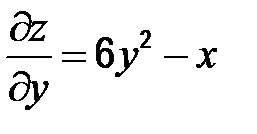Найдем значения частных производных в точке А (1; 2):

;     

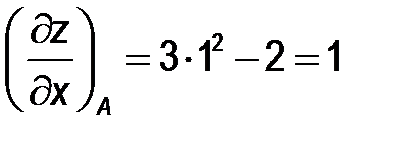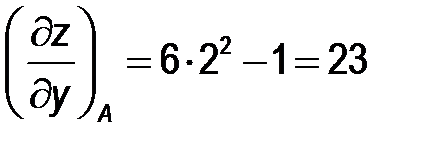
Ответ: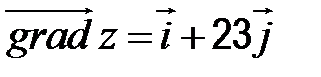

Вопросы для самоконтроля.

1. Дайте определение функции двух переменных.

2. Дайте определение частных производных.

3. Как вычисляются частные производные?

4. Дайте определение градиента функции.

Литература: [8] стр. 243-275, [4] стр. 304-310.

Примеры: [1] стр.81-95, [7] стр. 256-258.

ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ЭКЗАМЕНУ

1. Задача о площади криволинейной трапеции, приводящая к понятию определенного интеграла.

2. Понятие определенного интеграла, его геометрическая интерпретация. Свойства определенного интеграла. Теорема существования Формула Ньютона-Лейбница.

3. Методы вычисления определенного интеграла: подстановкой и по частям.

4. Вычисление площади плоской фигуры с помощью определенного интеграла.

5. Несобственный интеграл 1-го рода, его геометрическая интерпретация.

6. Несобственный интеграл 2-го рода, его геометрическая интерпретация.

7. Основные понятия теории обыкновенных дифференциальных уравнений

8. Дифференциальные уравнения 1-го порядка: различные формы представления; понятие общего и частного решений, их геометрическая интерпретация; задача Коши, теорема Коши.

9. Определение дифференциального уравнения с разделяющими переменными, метод его интегрирования.

10. Понятие однородного дифференциального уравнения 1-го порядка, метод его интегрирования.

11. Понятие линейного дифференциального уравнения 1-го порядка и уравнения Бернулли. Метод их интегрирования.

12. Определение дифференциального уравнения n-го порядка: общее и частное решение; задача Коши, её геометрическая интерпретация для уравнений 2-го порядка.

13. Дифференциальные уравнения высших порядков, допускающие понижение порядка, методы их интегрирования.

14. Определение линейного однородного дифференциального уравнения 2-го порядка с постоянными коэффициентами. Вид его общего решения в зависимости от вида корней характеристического уравнения.

15. Линейные неоднородные дифференциальные уравнения 2-го порядка.

16. Определение числового ряда. Понятие n-ой частичной суммы ряда. Определение суммы ряда. Свойства числовых рядов.

17. Необходимый признак сходимости числового ряда.

18. Достаточные признаки сходимости знакопостоянных рядов: признак Даламбера, радикальный признак Коши, интегральный признак Коши, признак сравнения в предельной форме.

19. Определение знакопеременных числовых рядов. Теорема об абсолютной сходимости знакопеременного ряда.

20. Определение знакочередующихся рядов. Признак Лейбница.

21. Определение функционального и степенного ряда, области сходимости и радиуса сходимости степенного ряда. Теорема Абеля, следствия из неё.

22. Свойства степенных рядов. Приложения степенных рядов.

23. Функции двух переменных. Основные понятия. Частные производные.

24. Градиент функции.

 

СПИСОК ИСПОЛЬЗОВАННОЙ И РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ.

 

Основная литература:

1. Данко, П.Е. Высшая математика в упражнениях и задачах. В 2 –х ч. Ч. I: Учеб. пособие для втузов./П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова – Москва: ОНИКС: Мир и Образование, 2009 – 368с.

2. Данко, П.Е. Высшая математика в упражнениях и задачах. В 2 –х ч. Ч. II: Учеб. пособие для втузов./ П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова – Москва: ОНИКС: Мир и Образование, 2009 – 448с.

3. Клетеник Д.В. Сборник задач по аналитической геометрии: Уч. пособие для втузов./ Д.В.Клетеник – СПб., Изд-во «Профессия», 2007. – 199 стр., ил.

4. Письменный Д.Т. Конспект лекций по высшей математике: полный курс.–4-е изд./ Д.Т. Письменный –М.: Айрис-пресс, 2011.–608 с. – (Высшее образование).

 

Дополнительная литература:

5. Кремер Н.Ш. Практикум по высшей математике для экономистов. Учебник./ Н.Ш.Кремер – М.: Юнити, 2004.

6. Кремер Н.Ш. Высшая математика для экономистов. Учебник. / Н.Ш.Кремер, Б.А. Путко, И.М.Тришин, М.Н.Фридман – М.: Юнити, 1998.

7. Минорский В.П. Сборник задач по высшей математике. Учеб. пособие для вузов. / В.П.Минорский – М.: Наука, 1997. – 285 с.

8. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. В 2-х томах, том 1, изд. «Наука», М.,1985 г., 456 стр. с илл.

9. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. В 2-х томах, том 2, изд. «Наука», М.,1985 г., 456 стр. с илл.

 

 

 Тамара Григорьевна Ершова, Ирина Александровна Драчева

 

МАТЕМАТИЧЕСКИЙ АНАЛИЗ

 2 часть

 

Практикум

по самостоятельной работе и выполнению контрольных работ

для студентов направления подготовки 38.03.01 «Экономика»

заочной формы обучения

 

Тираж ___экз.   Подписано к печати __________ Заказ № ____ Объем 0,8 п.л.

Изд-во «Керченский государственный морской технологический университет»

298309, Керчь, ул. Орджоникидзе, 82