Первообразная. Интеграл. Комбинаторика, статистика и теория вероятностей

Цель задания: расширить и углубить знания по теме, отработать практические умения и навыки, применяя их при решении прикладных задач с помощью интегрального исчисления.

Задание для самоподготовки:

1. Повторить таблицу интегралов и их свойства.

2. Дать определение и определенного и неопределенного интегралов.

3. Формула для вычисления определенного интеграла.

4. Повторить физический и геометрический смысл определенного интеграла.

5. Определение криволинейной трапеции.

6. Выполнить практические задания №1 и №2.

 

Задания №1

Номер задания соответствует номеру по списку классного журнала.

Вычислить неопределенные интегралы

1.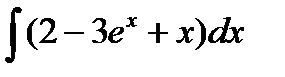
2.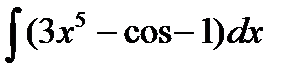
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.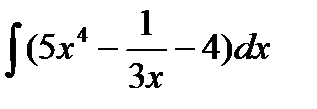
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.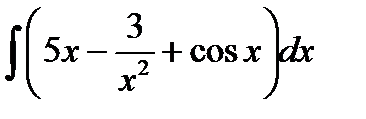
28.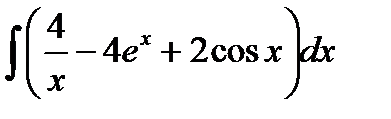
29.
30.

      

Задание №2

Номер задания соответствует номеру по списку классного журнала.

Вычислить площадь фигуры, ограниченную линиями.

1. ,

2. ,

3. ,  

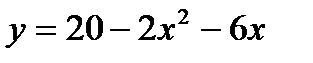
4. , , ,

5. , ,

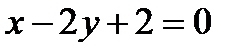6. ,

7. ,

8. , ,

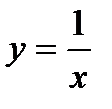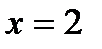
9. ,

10. , ,

11. , , ,

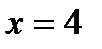12. ,

13. , , ,

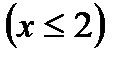
14. , ,

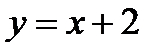15. , ,

16. ,

17. , ,

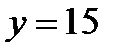18. ,

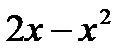
19. ,

20. ,

21. ,

22. ,

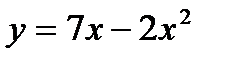23. , ,

24. , ,

25. , ,

26. , , осью  OX и

27. ,

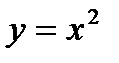28. ,

29. , , ,

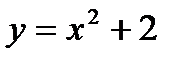30. , , ,

Вопросы самоконтроля

1. Дать определение определенного и неопределенного интегралов.

2. Что вычисляют с помощью формулы Ньютона-Лейбница?

3. Сформулировать физический и геометрический смысл определенного интеграла.

4. Какую фигуру называют криволинейной трапецией.

5. Как вычислить площадь криволинейной трапеции расположенной выше оси абсцисс и ниже оси абсцисс.

Раздел №6

Декартовы координаты и векторы в пространстве.