А) Параллельные силы направлены в одну сторону.
 |
Рассмотрим твердое тело, на которое действуют две параллельные силы
 и
и  , приложенные в точках
, приложенные в точках 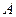 и
и 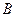 тела (рис.37а). Требуется определить модуль и точку приложения равнодействующей этих двух сил.
тела (рис.37а). Требуется определить модуль и точку приложения равнодействующей этих двух сил.
Пользуясь аксиомами 1 и 2 статики, перейдем от данной системы параллельных сил к эквивалентной системе сходящихся сил  и
и  . Для этого приложим в точках
. Для этого приложим в точках 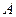 и
и 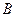 прямопротивоположные силы
прямопротивоположные силы  и
и  , направленные вдоль прямой
, направленные вдоль прямой  и сложим силы
и сложим силы  ,
,  и
и  ,
,  по аксиоме 3 (рис. 37б).
по аксиоме 3 (рис. 37б).
33
Полученные в результате такого сложения силы  и
и  , переносим вдоль линий их действия в точку
, переносим вдоль линий их действия в точку  и раскладываем обратно на составляющие
и раскладываем обратно на составляющие  ,
, 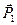 и
и  ,
,  . Прямопротивоположные силы
. Прямопротивоположные силы  и
и  можно отбросить, при этом состояние тела не изменится (рис. 37в).
можно отбросить, при этом состояние тела не изменится (рис. 37в).
В результате в точке  получаем две силы
получаем две силы  и
и  направленные вдоль одной прямой. Перенесем эти силы вдоль линии их действия в точку
направленные вдоль одной прямой. Перенесем эти силы вдоль линии их действия в точку  и находим их равнодействующую
и находим их равнодействующую  , модуль которой равен
, модуль которой равен  (рис. 37г). Для определения точки приложения силы
(рис. 37г). Для определения точки приложения силы  (точки
(точки 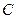 ) рассмотрим подобные треугольники
) рассмотрим подобные треугольники 
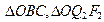 (рис. 37в).
(рис. 37в). 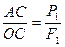 ,
, 
или учитывая, что  ,
,  .
. 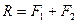 ,
,  , получаем
, получаем  . (10)
. (10)
Таким образом, равнодействующая двух действующих на абсолютно твердое тело параллельных сил, направленных в одну сторону, равна по модулю сумме модулей слагаемых сил, им параллельна и направлена в ту же сторону. Линия действия равнодействующей проходит между точками приложения слагаемых сил на расстояниях от этих точек, обратно пропорциональных силам.
 2020-05-12
2020-05-12 185
185








