2020-05-12
1058
Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы одновременно выполнялись условия 
и 
.
Эти условия являются необходимыми, т.к. если какое – нибудь из них не выполняется, то система действующих на тело сил приводится либо к паре сил (
), либо к равнодействующей (
), и следовательно, не является уравновешенной. Одновременно эти условия являются достаточными, т.к. при 
система может приводится только к паре с моментом 
, а т.к. 
, то имеет место равновесие.
Определим аналитические условия равновесия. Эти условия можно получить в трех различных формах.
1. Основная форма условий равновесия произвольной плоской системы сил.
Для равновесия произвольной плоской системы сил, необходимо и достаточно, чтобы суммы проекций всех сил на каждую из двух координатных осей и сумма их моментов относительно любого центра, лежащего в плоскости действия сил, были равны нулю.
 |
, 
, 
, 
. Тогда 2. Вторая форма условий равновесия произвольной плоской системы сил.
 |
Для равновесия произвольной плоской системы сил, необходимо и достаточно, чтобы суммы моментов всех сил относительно каких - нибудь двух центров
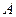и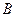 
и сумма проекций этих сил на ось 
, не перпендикулярную 
, были равны нулю. Эта форма записи содержит ограничение, чтобыось была не перпендикулярна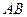 
. Суть этого ограничения состоит в следующем. Допустим, что в результате приведения плоской системе сил, она привилась к равнодействующей 
, причем линия действия этой силы может проходить через центры 
и 
. Тогда, если мы ось 
направим перпендикулярно 
, то
28
проекция равнодействующей на эту ось будет равна нулю. Следовательно, все условия равновесия выполняются, но система в равновесии не находится. Значит, для того, чтобы «поймать» этот вектор 
ось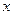 
должна составлять с линией любой угол, кроме прямого.
3. Третья форма условий равновесия произвольной плоской системы сил.
 |
Для равновесия произвольной плоской системы сил, необходимо и достаточно, чтобы суммы моментов всех сил относительно каких - нибудь трех центров
, не лежащих на одной линии, были равны нулю. Эта форма записи также содержит ограничение, которое объяснялось во второй форме записи.
