Моделирование группы несовместных событий

Пусть группа несовместных событий 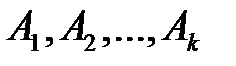, наступление которых необходимо исследовать. Известны вероятности наступления этих событий 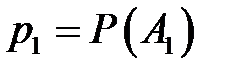, ,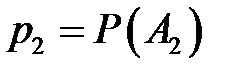…, 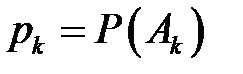. Если события несовместны, то 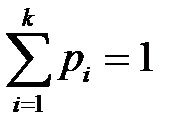. Допустим, что 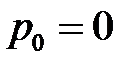. На отрезке  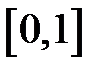числовой оси отметим значения этих вероятностей (рис.2).

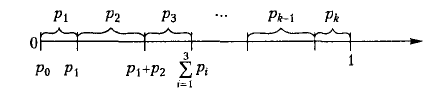
Рис. 2. Моделирование группы несовместных событий

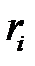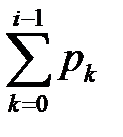Если полученное от генератора случайных чисел значение  попадает в интервал от   до 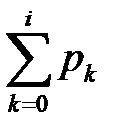, считаем, что произошло событие 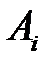. Такую процедуру называют определением результата испытания по жребию. Она основана на формуле:

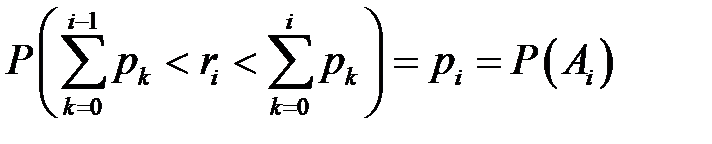, где .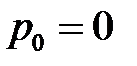

Эта модель часто применяется в теории принятия решений и хорошо воспроизводит процессы выбора одной из многих альтернатив в компьютерных играх, разветвления потоков информации в узлах сети в нескольких направлениях, выбор одного из многих устройств обслуживания в СМО и др.

Моделирование условного события

Условное событие 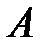 – это событие, которое происходит с вероятностью  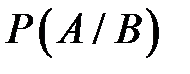только при условии, что наступило событие 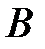. (рис.3).

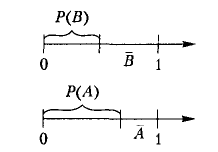
Рис.3 Моделирование появления условного события

В этом случае задаётся вероятность 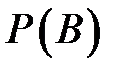 наступления события 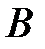. Моделирование появления условного события 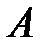: сначала случайное число 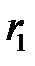, полученное от генератора случайных чисел, используется для моделирования появления события 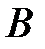. Событие  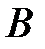наступает в том случае, если выполняется неравенство 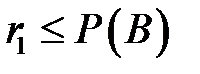. Появление события  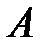моделируется с помощью числа 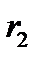. Для этого проверяется условие 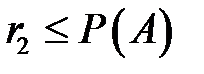, при выполнении которого принимается решение, что событие  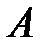произошло. Если же событие  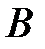не появилось (т.е. наступает событие 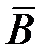), то появление события  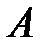моделировать не нужно. Таким образом, можно сократить общее количество испытаний.