Двухлучевая интерференция

Интерференция волн - явление наложения двух когерентных волн, при котором наступает устойчивое во времени их взаимное усиление в одних точках пространства и послабления в других в зависимости от соотношения фаз этих волн. Волны должны иметь одинаковый период и неизменный сдвиг по фазе, такие волны называются когерентными.

Естественные источники света не являются когерентными

Считаем, что в некоторой точке пространства две волны одинаковой частоты возбуждают колебания одинакового направления.

φ2

φ1

А0

А01

А02

A₁= A₀₁cos(ωt + φ₁)

A₂= A₀₂cos(ωt + φ₂)

Тогда амплитуда результирующего колебания (по теореме косинусов)

 

A²₀ =A²₀₁+A²₀₂+ 2 A₀₁A₀₂ cosδ

 где d=j₂-j₁

если , где m=±(0,1,2,…) то имеет место максимум суммарной амплитуды                                

,

Если , то минимум

 

Если δ=const, тогда такие волны называются когерентными.

В общем случае δ=var и среднее по времени <cosδ>=0. Тогда

<A² >=<A²₀₁> + <A²₀₂>

но интенсивность волны I∞A² , поэтому            I=I₁+I₂

Если волны когерентные .

Так как cosδ лежит в пределах 1 < cosδ< 1, то в пространстве происходит перераспределение светового потока, вследствие чего в одних местах возникают максимумы, а во вторых - минимумы. Если амплитуды (интенсивности) одинаковые тогда

Imax=0      Imax=4I

Для некогерентного источника интенсивность везде одинаковая

I=I₁+I₂= const

Рассмотрим две распространяющиеся волны одного направления.

1

2

r1

r2

n1

n2

Считаем, что из т. 1 в т. 2 двумя различными путями распространяется две когерентные волны. Для первой волны: путь r₁ и показатель преломления среды n₁, для второй: путь r₂ и показатель преломления среды n₂. Полагая, что начальная фаза колебаний равна нулю, в т. 2 получим:

          

Обозначив фазу волны как:

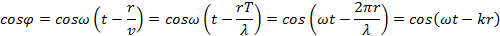
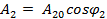
Тогда разность фаз двух волн в точке наблюдения будет равна

 

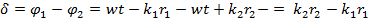
, где   

 

. – где

L - оптическая длина пути 

Δ- оптическая разность хода

Если разность фаз δ кратна 2π, тогда колебания в т. 2 приходят в фазе и усиливаются, то есть оптическая разность хода кратная  λ, имеет место максимум:

 

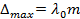,     при m=0; ±1; ± 2..

Если оптическая разность хода кратна нечётному числу λ/2, то есть при

δ=(2m+1)π, имеет место минимум

  

Можно получить аналогичный результат простым сложением колебаний:

При сложении двух когерентных волн (для простоты амплитуды гармонических колебаний принимаются одинаковым ,

По принципу суперпозиции их сложение

если гармонические колебания выражаются через sin, то вместе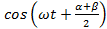

имеем sin

 

Если , Тогда   принимает максимальное значение в точках 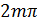. Здесь m=±1, ±2, ±3,.. порядок максимума.

,     

 

φ

r1

r2

x

L

d

Рассмотрим две цилиндрические когерентные волны от источников S1 и S2 которые имеют вид параллельных узких щелей или нитей. Область, в которой эти волны пересекаются называется полем интерференции - здесь наблюдаем чередование max и min интенсивности света. Рассчитаем ширину полос, которые получаем на экране. Считаем, что колебание в т.1 и 2 - синфазны.

Из рисунка видно

                                        

                                        

                

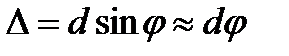
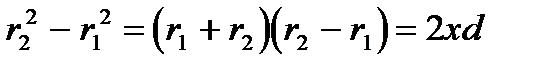
Как будет показано ниже, для наблюдения интерференционной картины необходимо, чтобы d<<L и x<<L или

 

- где, n -показатель преломления

Расстояние между двумя соседними max – это расстояние между двумя интерференционными полосами:

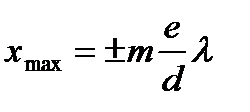, при m=0,1,2...

-где - длина волны в среде

Расстояние между двумя соседними min - ширина интерференционной полосы.

 , при m = 0,1,2,...

Тогда из этого следует, что расстояние между полосами и ширина равны:

 

То есть расстояние между полосами растет с убыванием d. Если d≈L, то отдельные полосы будут практически не различимы. Поэтому необходимое условие d<<L

Рассмотрим распределение освещенности вдоль экрана. Так как мы считаем, что ,тo

Так как

Полученные выражения справедливы для монохроматической волны. Если интерферирует белый свет, то, Δx зависит от λ. В центре при x=0 всегда будет max для всех цветов (белый). По мере отдаления max разных цветов будут смещаться друг от друга и картина будет размытой (цветной)

В монохроматичном свете число различимых интерференционных полос растет.