2.1. Формула Бернулли.
Предположим что производится 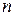 независимых испытаний, в каждом из которых событие
независимых испытаний, в каждом из которых событие  может либо наступит либо не наступить. Пусть вероятность наступления события
может либо наступит либо не наступить. Пусть вероятность наступления события  в каждом испытании равна
в каждом испытании равна  , тогда вероятность того что это событие не наступит:
, тогда вероятность того что это событие не наступит:  .
.
Поставим перед собой следующую задачу: вычислить вероятность того, что при  испытаниях, событие
испытаниях, событие  осуществится
осуществится  раз и, следовательно, не осуществится
раз и, следовательно, не осуществится  раз. При этом, не требуется чтобы событие
раз. При этом, не требуется чтобы событие  повто-рилось ровно
повто-рилось ровно  раз в определенной последовательности. Последовательность может меняться включая появление и не появление события
раз в определенной последовательности. Последовательность может меняться включая появление и не появление события  , т. е., другими словами, появление события
, т. е., другими словами, появление события  . Эта вероятность вычисляется по следующей формуле получившей название формулы Бернулли:
. Эта вероятность вычисляется по следующей формуле получившей название формулы Бернулли:
 (15)
(15)
Замечание: Если требуется вычислить вероятность наступления события “  ” от “
” от “  “ до “
“ до “  “ раз при “
“ раз при “  ” независимых испытаниях, то (15) при-нимает вид:
” независимых испытаниях, то (15) при-нимает вид:
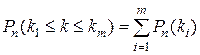 (16)
(16)
При решении каждой задачи данного параграфа, прежде всего, необходимо установить, что рассматриваемый эксперимент удовлетворяет схеме Бернулли, т. е. необходимо проверить, что: 1) проводимые испытания независимы; 2) каждое испытание имеет два исхода; 3) вероятность появления события в каждом испытании постоянна и равна  .
.
При больших значениях  , вычисление вероятностей
, вычисление вероятностей  с помощью формулы Бернулли оказывается довольно сложным. Поэтому оно проводится с помощью других приближенных формул.
с помощью формулы Бернулли оказывается довольно сложным. Поэтому оно проводится с помощью других приближенных формул.
Формула Пуассона.
В том случае, если количество испытаний велико  , а вероятность события мала
, а вероятность события мала 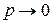 , так что
, так что  ,
,  и
и  . то используется приближенная формула Пуассона:
. то используется приближенная формула Пуассона:
 (17)
(17)
 2020-05-21
2020-05-21 492
492








