2020-05-21
5059
Данная теорема представляет собой группу теорем, устанавливающих условия, при которых возникает нормальный закон распределения. В наиболее простой форме, относящейся к случаю одинаково распределенных слагаемых, она формулируется следующим образом:
Если 
, 
,…, 
являются независимыми случайными величинами, которые имеют один и тот же закон распределения с математическим ожиданием 
и дисперсией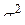 
, то при неограниченном увеличении 
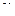закон распределения суммы 
приближается к нормальному.
Центральная предельная теорема справедлива и для неодинаково распределенных слагаемых:
Теорема Ляпунова. В том случае, если , ,…, являются независимыми случайными величинами, каждая из которых имеет математическое ожидание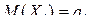 
, дисперсию 
, абсолютный центральный момент третьего порядка определяемый выражением 
и выполняется условие: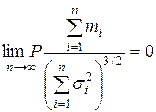 
. то закон распределения суммы 
, при 
неограниченно приближается к нормальному с математическим ожиданием 
и дисперсией 
.
Пример 35. При стрельбе по мишени, представляющей собой круг радиуса 30 см, средняя величина отклонения от центра мишени равна 6 см. С помощью неравенства Маркова, оценить вероятность поражения мишени при одном выстреле.
Решение. Вполне очевидно, что мишень будет поражена в том случае, если произойдет событие (
). Средняя величина отклонения от центра мишени равна . Тогда, с помощью формулы (28) получаем следующую оценку:
.
Пример 36. У деталей изготовленной партии, среднее значение длины равно 50 см, а среднее квадратическое отклонение равно 0,2 см. Оценить снизу вероятность того, что длина наудачу взятой детали окажется не менее 49,5 см и не более 50,5 см.
Решение. Случайная величина 
, которой является длина детали, имеет конечную дисперсию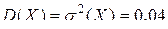 
и математическое ожидание 
. Поэтому, для оценки снизу вероятности используем неравенство Чебышева (24). Поскольку 
, следовательно 
, откуда 
.
Т. е.,: 
.
Пример 37. Для определения средней продолжительности горения электроламп в партии из 200 одинаковых ящиков было взято на выборку по одной лампе из каждого ящика. Оценить вероятность того, что средняя продолжительность горения отобранных 200 электроламп отличается от средней продолжительности горения ламп во всей партии не более чем на 5 часов (по абсолютной величине), если известно, что среднее квадратическое отклонение продолжительности горения ламп в каждом ящике меньше 7 часов.
Решение. Пусть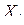 
это продолжительность горении электролампы взятой из i-го ящика. По условию, дисперсия 
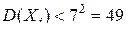. К рассматриваемой последовательности случайных величин можно применить теорему Чебышева, поскольку 1) величины независимы; 2) дисперсии ограничены: 
(
; 3) математические ожидания существуют.
Очевидно, что средняя продолжительность горения отобранных ламп: 
, а средняя продолжительность горения ламп во всей партии: 
. Тогда вероятность искомого события по формуле (26):
т. е. не менее чем 
.
Пример 38. Математическое ожидание числа очков, выпавших при бросании игральной кости, равно 3,5, а дисперсия равна (35/12). Игральная кость подбрасывается 350 раз. Оценить вероятность того, что среднее арифметическое числа выпавших очков отклонится от математического ожидания по абсолютной величине не более чем на 0,2.
Решение. Случайная величина 
(
представляет собой число очков, выпавших на верхней грани игральной кости. Данные случайные величины: 1) независимы, 2) имеют ограниченные дисперсии, 3) имеют одно и то же математическое ожидание. Искомую оценку получим, используя неравенство 27, в котором 
, 
, 
, 
.
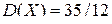Пример 39. Оценить вероятность того,что в результате подбрасывания игральной кости в течение 320 раз относительная частота появления на верхней грани пяти очков отклонится от вероятности этого события (по абсолютной величине) не более чем на 0,03.
Решение. Рассматриваемые испытания удовлетворяют схемеБернулли: 1) испытания независимы; 2) каждое испытание имеет два исхода (на верхней грани появилось 5 очков, на верхней грани не появилось 5 очков), 3) вероятность появления 5 очков в каждом испытании постоянна и равна 
. Поэтому, для оценки события 
, где 
относительная частота появления 5 очков, можно применить неравенство (28), где 
, , 
, 
.
.
4.6. Задачи для самостоятельного решения
161. [1] Используя неравенство Чебышева, оценить вероятность того, что случайная величина отклонится от своего математического ожидания менее чем на три средних квадратических отклонения.
(Ответ: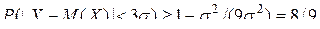 
).
162. [1] В осветительную сеть параллельно включено 20 ламп. Вероятность того, что за время 
лампа будет включена, равна 0,8. Пользуясь неравенством Чебышева, оценить вероятность того, что абсолютная величина разности между числом включенных ламп и средним числом (математическим ожиданием) включенных ламп за время окажется: а) меньше трех; б) не меньше трех.
(Ответ: а) 
; б) 
).
163. [1] Вероятность появления события в каждом испытании равна 1/4. Используя неравенство Чебышева, оценить вероятность того, что число появлений события заключено в пределах от 150 до 250, если будет произведено 800 испытаний. (Ответ: 
).
164. [2] Математическое ожидание начальной скорости снаряда 600 м/с. Оценить вероятность того, что могут наблюдаться значения начальной скорости, превышающие 900 м/с.
165. [2] Средняя температура в квартире, подключенной к теплоцентрали, в период отопительного сезона составляет 200С, а среднее квадратическое отклонение равно 20С. Оценить вероятность того, что температура в квартире отклонится от средней по абсолютной величине не более чем на 50С. (Ответ: 
).
166. [2] Игральная кость подбрасывается 180 раз. Используя неравенство Чебышева, оценить вероятность того, что 5 очков появится от 24 до 36 раз. Оценить вероятность этого же события с помощью интегральной теоремы Лапласа. (Ответ: 
; 
).
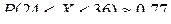167. [2] Вероятность получения с конвейера изделия высшего качества равна 0,6. Используя неравенство Чебышева и интегральную теорему Лапласа, оценить вероятность наличия от 340 до 380 изделий высшего качества в партии из 600 изделий. Сравнить полученные результаты. (Ответ: 
; 
).
168. [2] Вероятность получения с конвейера изделия высшего качества равна 0,8. Проверяется 800 изделий. Случайная величина 
число изделий высшего качества. Указать промежуток, в котором значения этой случайной величины можно ожидать с вероятностью, не меньшей 0,5. (Ответ: 
).
169. [2] Дисперсия каждой из независимых случайных величин , означающей горение электролампочки, не превышает 20 час. Сколько нужно взять для испытания лампочек, чтобы вероятность того, что абсолютное отклонение средней продолжительности горения лампочки от средней арифметической их математических ожиданий не превышает одного часа, была не меньше 0,95? (Ответ: 
).
170. [2] Каждая из 2000 независимых случайных величин (
имеет дисперсию, равную 4,5. Математические ожидания этих случайных величин одинаковы. Оценить вероятность того, что среднее арифметическое случайных величин отклонится от математического ожидания по абсолютной величине не более чем на 0,15.
(Ответ: 
).
171. [4] Электростанция обслуживает сеть из 1600 электроламп, вероятность включения каждой из которых вечером равна 0,9. Оценить с помощью неравенства Чебышева вероятность того, что число ламп, включенных в сеть вечером, отличается от своего математического ожидания не более чем на 100 (по абсолютной величине).Найти вероятность того же события, используя следствие из интегральной теоремы Муавра-Лапласа. (Ответ: 
; 
).
172. [4] Вероятность сдачи в срок всех экзаменов студентом факультета равна 0,7. С помощью неравенства Чебышева оценить вероятность того, что доля сдавших в срок все экзамены из 2000 студентов заключена в границах от 0,66 до 0,74. (Ответ: 
).
173. [4] Вероятность того, что акции, переданные на депозит, будут востребованы, равна 0,08. Оценить с помощью неравенства Чебышева вероятность того, что среди 1000 клиентов от 70 до 90 востребуют свои акции. (Ответ: 
).
174. [4] Оценить вероятность того, что отклонение любой случайной величины от ее математического ожидания будет не более двух средних квадратических отклонений (по абсолютной величине). (Ответ: 
).
175. [4] Сколько нужно произвести измерений, чтобы с вероятностью, равной 0,9973, утверждать, что погрешность средней арифметической результатов этих измерений не превысит 0,01, если измерение характеризуется средним квадратическим отклонением, равным 0,03? (Ответ: 
).
176. [4] Отделение банка обслуживает в среднем 100 клиентов в день. Оценить вероятность того, что сегодня в отделении банка будет обслужено: а) не более 200 клиентов; б) более 150 клиентов. (Ответ: а) 
; б) 
).
177. [4] В целях контроля, из партии в 100 ящиков взяли по одной детали из каждого ящика и измерили их длину. Требуется оценить вероятность того, что вычисленная по данным выборки средняя длина детали отличается от средней длины детали во всей партии не более чем на 0,3 мм, если известно, сто среднее квадратическое отклонение не превышает 0,8 мм. (Ответ: 
).
178. [4] В течение времени 
эксплуатируется 500 приборов. Каждый прибор имеет надежность 0,98 и выходит из строя независимо от других. Оценить с помощью неравенства Чебышева вероятность того, что доля надежных приборов отличается от 0,98 не более чем на 0,1 (по абсолютной величине). (Ответ: 
).
179. ([4] В среднем 10% работоспособного населения некоторого региона – безработные. Оценить с помощью неравенства Чебышева вероятность того, что уровень безработицы среди обследованных 10000 работоспособных жителей города будет в пределах от 9 до 11% (включительно). (Ответ: 
).
180. [4] Опыт работы страховой компании показывает, что страховой случай приходится примерно на каждый пятый договор. Оценить с помощью неравенства Чебышева необходимое количество договоров, которые следует заключить, чтобы с вероятностью 0,9 можно было утверждать, что доля страховых случаев отклонится от 0,1 не более чем на 0,01 (по абсолютной величине). Уточнить ответ с помощью следствия из интегральной теоремы Муавра-Лапласа. (Ответ: 
; 
).
181. [3] Используя неравенство Чебышева, найти вероятность того, что частота появления герба при ста бросаниях монеты отклонится от вероятности не более, чем на 0,1; Сравнить с вероятностью, поученной с помощью применения интегральной теоремы Муавра-Лапласа.
(Ответ: 
).
182. [3] Дисперсия каждой из 2500 независимых случайных величин не превосходит 5. Оценить вероятность того, что отклонение среднего арифметического этих случайных величин от среднего арифметического их математических ожиданий не превзойдет 0,4.
Ответ:
.
183. [3] Среднее квадратическое отклонение каждой из 2134 независимых случайных величин не превосходит 4. Оценить вероятность того, что отклонение среднего арифметического этих величин от среднего арифметического их математических ожиданий не превзойдет о,5. (Ответ: 
).
184. [3] За значение некоторой величины принимают среднее арифметическое достаточно большого числа ее измерений. Предполагая, что среднее квадратическое отклонение возможных результатов каждого измерения не превосходит 1, оценить вероятность того, что при 1000 измерений этой величины отклонение найденного ее значения от истинного не превосходит 0,1 единицы. (Ответ: 
).
185. [3] Технический контролер проверяет партию однотипных приборов. С вероятностью 0,01 прибор может иметь дефект А и, независимо от этого, с вероятностью 0,02 – дефект В.
а) В каких границах будет заключено практически наверняка число бракованных изделий в партии из 1000 штук, если за вероятность практической достоверности принимается 0,997?
б) Решить тот же вопрос, применяя интегральную теорему Муавра-Лапласа.
(Ответ: а) 
; б). 
).
186. [3] Изнашивание орудия при стрельбе таково, что каждый выстрел уменьшает вероятность попадания в цель на 1%. При первом выстреле эта вероятность равна 0,8. Производится 100 выстрелов. Найти границы, в которых с вероятностью 0,85 будет заключено число попаданий. (Ответ: 
).
187. [3] Математическое ожидание скорости ветра на данной высоте равно 25 км/час. Какие скорости ветра можно ожидать на этой высоте с вероятностью, не меньшей 0,9? (Ответ: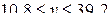 
км/час. ).
188. [3] Математическое ожидание количества выпадающих в течение года в данной местности осадков составляет 55 см. Оценить вероятность того, что в этой местности осадков выпадет 175 см. (Ответ; 0,3).
189. [3] Средний расход воды в населенном пункте составляет 50000 л в день. Оценить вероятность того, что в этом населенном пункте в данный день расход воды не превысит 150000 л. (Ответ: 2.3)).
190. [3] Число солнечных дней в году для данной местности является случайной величиной с математическим ожиданием, равным 75 дням. Оценить вероятность того, что в течение года в этой местности будет не более 200 солнечных дней. (Ответ: 
)).
191. [3] Случайная величина 
имеет математическое ожидание 
и среднее квадратическое отклонение 
. С помощью неравенства Чебышева оценить вероятность неравенства: 
(Ответ: 
).
192. [3] Среднее квадратическое отклонение ошибки измерения курса самолета 
. Считая математическое ожидание ошибки измерения равным нулю, оценить вероятность того, что ошибка при данном измерении курса самолета будет более 
. (Ответ: 0,16.).
193. [3] Среднее квадратическое отклонение ошибки измерения азимута равно 
(а математическое ожидание равно нулю). Оценить вероятность того, что ошибка среднего арифметического трех независимых измерений не превзойдет 
. (Ответ: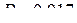 
).
194. [3] Вероятность некоторого события А в каждом испытании из серии 
независимых испытаний равна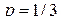 
, Используя неравенство Чебышева, оценить вероятность того, что частота этого события отклонится от его вероятности по абсолютной величине не более, чем на 0,01, если будет произведено а) 
испытаний; б) 
. Сравнить полученные оценки с результатами применения интегральной теоремы Муавра-Лапласа. (Ответ: а) 
; б ) 
; в) 
; г) 
).
195. [3] Среднее значение скорости ветра у земли в данном пункте равно 16 км/час. Оценить с помощью первой формы неравенства Чебышева вероятность того, что в этом пункте скорость ветра (при одном наблюдении) не превысит 80 км/час. (Ответ:. 
).
196. [6] Вероятность произрастания зерна равна 0,96. В соответствии с неравенством Чебышева оценить вероятность того, что число не проращенных зерен из 2000 находится в границах от 60 до 100. Сравнить полученные оценки с результатами применения интегральной теоремы Муавра-Лапласа. (Ответ: 
; 
).
197. [6] Среднее изменение курса акции компании в течение одних биржевых торгов составляет 0,3%. С помощью неравенства Маркова оценить вероятность того, что на ближайших торгах курс изменится более чем на 3%. (Ответ: 
)..
198. [6] Среднее число просмотров в день видеоролика составило 50000. При помощи неравенства Маркова оценить вероятность того, что число просмотров в день не превосходит 120000. (Ответ: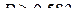 
)..
199. [6] Можно ли с вероятностью большей, чем 0,97 утверждать, что при 1000 подбрасываний монеты количество выпадений герба будет заключено в пределах от 400 до 600. Задачу решить с помощью неравенства Чебышева и интегральной теоремы Муавра-Лапласа. Сравнить ответы. (Ответ: да, 
; 
).
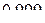200. [6] Игральную кость бросили 4200 раз. Оценить вероятность того, что 3 очка выпало больше 650 раз и меньше 750 раз. Задачу решить при помощи неравенства Чебышева и интегральной теоремы Муавра-Лапласа. Сравнить ответы. (Ответ: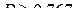 
; 
).
ПРИЛОЖЕНИЕ
Значение функций Гаусса 
и Лапласа 
.
|
| 
| 
|
|
| )
|
| 0,0 | 0,3989 | 0,0000 | 1,55 | 0,1200 | 0,4394 |
| 0,05 | 0,3984 | 0,0199 | 1,60 | 0,1109 | 0,4452 |
| 0,10 | 0,3970 | 0,0398 | 1,65 | 0,1023 | 0,4505 |
| 0,15 | 0,3945 | 0,0596 | 1,70 | 0,0940 | 0,4554 |
| 0,20 | 0,3910 | 0,0793 | 1,75 | 0,0863 | 0,4599 |
| 0,25 | 0,3867 | 0,0987 | 1,80 | 0,0790 | 0,4641 |
| 0,30 | 0,3814 | 0,1179 | 1,85 | 0,0721 | 0,4678 |
| 0,35 | 0,3752 | 0,1368 | 1,90 | 0,0656 | 0,4713 |
| 0,40 | 0,3683 | 0,1554 | 1,95 | 0,0596 | 0,4744 |
| 0,45 | 0,3605 | 0,1736 | 2,00 | 0,0540 | 0,4772 |
| 0,50 | 0,3521 | 0,1915 | 2,10 | 0,0440 | 0,4821 |
| 0,55 | 0,3429 | 0,2088 | 2,20 | 0,0355 | 0,4861 |
| 0,60 | 0,3332 | 0,2257 | 2,30 | 0,0283 | 0,4893 |
| 0,65 | 0,3230 | 0,2422 | 2,40 | 0,0224 | 0,4918 |
| 0,70 | 0,3123 | 0,2580 | 2,50 | 0,0175 | 0,4938 |
| 0,75 | 0,3011 | 0,2734 | 2,60 | 0,0136 | 0,4953 |
| 0,80 | 0,2897 | 0,2881 | 2,70 | 0,0104 | 0,4965 |
| 0,85 | 0,2780 | 0,3023 | 2,80 | 0,0079 | 0,4974 |
| 0,90 | 0,2661 | 0,3159 | 2,90 | 0,0060 | 0,4981 |
| 0,95 | 0,2541 | 0,3289 | 3,00 | 0,00443 | 0,49865 |
| 1,00 | 0,2420 | 0,3413 | 3,10 | 0,00327 | 0,49903 |
| 1,05 | 0,2299 | 0,3531 | 3,20 | 0,00238 | 0,49931 |
| 1,10 | 0,2179 | 0,3643 | 3,30 | 0,00172 | 0,49952 |
| 1,15 | 0,2059 | 0,3749 | 3,40 | 0,00123 | 0,49966 |
| 1,20 | 0,1942 | 0,3849 | 3,50 | 0,00087 | 0,49977 |
| 1,25 | 0,1826 | 0,3944 | 3,60 | 0,00061 | 0,49984 |
| 1,30 | 0,1714 | 0,4032 | 3,70 | 0,00042 | 0,49989 |
| 1,35 | 0,1604 | 0,4115 | 3,80 | 0,00029 | 0,49993 |
| 1,40 | 0,1497 | 0,4192 | 3,90 | 0,00020 | 0,49995 |
| 1,45 | 0,1394 | 0,4265 | 4,00 | 0,0001338 | 0,499968 |
| 1,50 | 0,1295 | 0,4332 | 4,50 | 0,0000160 | 0,499997 |
| 5,00 | 0,0000015 | 0,49999997 |
