Приведем другое решение

Вариант № профиль.

1. Килограмм орехов стоит 75 рублей. Маша купила 4 кг 400 г орехов. Сколько рублей сдачи она должна получить с 350 рублей?

Решение.

Найдем стоимость покупки: 4 кг 400 г орехов стоит 4,4 · 75 = 330 рублей. Значит, с 350 рублей Маша получит сдачи 350 − 330 = 20 рублей.

 

Ответ: 20.

2. На рисунке показан график движения автомобиля по маршруту. На оси абсцисс откладывается время (в часах), на оси ординат — пройденный путь (в километрах). Найдите среднюю скорость движения автомобиля на данном маршруте. Ответ дайте в км/ч.

Решение.

Чтобы найти среднюю скорость, необходимо пройденное расстояние разделить на время прохождения: км/ч

 

Ответ: 50.

3. На клетчатой бумаге с размером клетки 1 1 изображён равносторонний треугольник. Найдите радиус описанной около него окружности.

Решение.

Радиус окружности, описанной вокруг равностороннего треугольника, равен двум третьим его высоты. Поэтому он равен 2.

 

Ответ: 2.

4. Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Физик» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Физик» выиграет жребий ровно два раза.

Решение.

Обозначим «1» ту сторону монеты, которая отвечает за выигрыш жребия «Физиком», другую сторону монеты обозначим «0». Тогда благоприятных комбинаций три: 110, 101, 011, а всего комбинаций 2³ = 8: 000, 001, 010, 011, 100, 101, 110, 111. Тем самым, искомая вероятность равна:

 

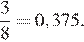
Ответ: 0,375.

5. Решите уравнение Если уравнение имеет более одного корня, в ответе укажите меньший из них.

Решение.

На ОДЗ перейдем к уравнению на основание логарифма:

Итак, на ОДЗ уравнение имеет только один корень.

 

Ответ: 12.

6. В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 12. Найдите ее среднюю линию.

Решение.

Треугольники и равнобедренные, так как и Следовательно, средняя линия равна

 

Ответ: 12.

7. На рисунке изображён график функции y = f (x). Функция 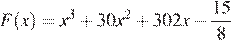— одна из первообразных функции y = f (x). Найдите площадь закрашенной фигуры.

Решение.

Площадь выделенной фигуры равна разности значений первообразных, вычисленных в точках и

Имеем:

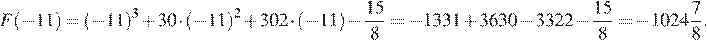
Приведем другое решение.

Вычисления можно было бы упростить, выделив полный куб:

что позволяет сразу же найти