Таблица основных пределов анализа

Замечание. Таблицу основных пределов необходимо выучить, так как незнание этих формул не позволит увидеть их в примере и приведет к дополнительным трудностям во время выполнения задания

Непрерывность функции

Два определения непрерывности функции в точке

Определение 1. Функция называется непрерывной в точке   , если предел функции в точке  равен значению функции в этой точке: .

Для любой точки разность  называется приращением аргумента; соответствующая разность значений функции называется приращением функции.

Определение 2 (эквивалентноепервому). Функция 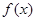 называется непрерывной в точке x ₀, если в этой точке бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, т.е. .

Свойства непрерывных функций

Теорема: с умма, разность и произведение конечного числа функций, непрерывных в точке x ₀, есть функция, неперерывная в точке x ₀. Частное от деления двух функций, непрерывных в точке x ₀, будет непрерывной функцией, если при x ₀делитель не обращается в ноль.

Теорема: если функция   непрерывна в точке x ₀, а функция   непрерывна в точке то сложная функция   будет непрерывной в точке x ₀.

Функция называется непрерывной на промежутке (a, b), если она непрерывна в каждой точке промежутка.

Все элементарные функции непрерывны в области своего определения.