При вычислении предела функции следует подставить в функцию предельное значение. Если при этом получим конечное число или бесконечность, то это значение и будет являться пределом функции.
Например, 
Зачастую появляются выражения, значение которых не определено. Такие выражения называют неопределенностями. Если получится неопределенность
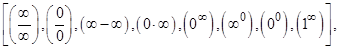
то ее следует раскрыть.
Раскрыть неопределенность — это значит вычислить предел, избавляясь от неопределенности с помощью преобразований, либо доказать, что предел не существует.
В некоторых примерах нам также приходится пользоваться переходом к пределу в показателе степени при постоянном основании. Если существует  , то при постоянном
, то при постоянном  имеет место формула
имеет место формула 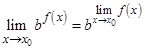 .
.
Короче (но менее точно): при постоянном основании можно переходить к пределу в показателе степени. При отыскании пределов вида  в случае, когда существуют конечные пределы
в случае, когда существуют конечные пределы  и
и  , имеет место формула
, имеет место формула

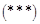
Замечание: в формуле 
 может обозначать и число, и один из символов
может обозначать и число, и один из символов  . Если в этой формуле
. Если в этой формуле 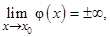 а
а  конечен, но не равен 1, то вопрос о пределе
конечен, но не равен 1, то вопрос о пределе  затруднений не вызывает. Случай, когда
затруднений не вызывает. Случай, когда  , а
, а 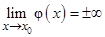 , рассматривается далее в типовых заданиях.
, рассматривается далее в типовых заданиях.
Пример 1. А. Доказать, что функции  и
и  являются бесконечно малыми при
являются бесконечно малыми при  Б. Сравнить бесконечно малые
Б. Сравнить бесконечно малые  и
и  :
:  .
.
Решение: А. Найдем пределы функций  и
и 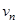 при
при 
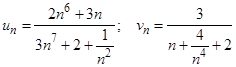 ;
; 
Для того чтобы раскрыть полученную неопределенность, надо разделить и числитель, и знаменатель дроби на  в наивысшей степени, встречающейся в данном выражении, т. е. на
в наивысшей степени, встречающейся в данном выражении, т. е. на 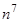 :
: 
аналогично получим 
Так как  то согласно определению, функции
то согласно определению, функции  и
и  являются бесконечно малыми при
являются бесконечно малыми при 
Б. Для того чтобы сравнить бесконечно малые функции  и
и  , надо найти предел их отношения при
, надо найти предел их отношения при 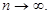
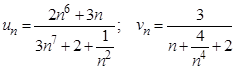 .
. 


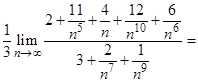
 Так как
Так как 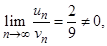 то данные функции
то данные функции  и
и  являются бесконечно малыми одного порядка при
являются бесконечно малыми одного порядка при 
Пример 2. Найти пределы функций (не пользуясь правилом Лопиталя).
.

Решение:
1)  Здесь числитель и знаменатель стремятся к нулю при
Здесь числитель и знаменатель стремятся к нулю при 
 Разложим числитель и знаменатель на множители, выделим общий множитель, который обращает их в ноль, затем сократим числитель и знаменатель на этот общий множитель. Разложение квадратных трехчленов на множители будем производить с помощью формулы
Разложим числитель и знаменатель на множители, выделим общий множитель, который обращает их в ноль, затем сократим числитель и знаменатель на этот общий множитель. Разложение квадратных трехчленов на множители будем производить с помощью формулы
 , где
, где  .
.
Найдем корни: 
 ;
;

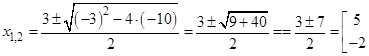 .
.
Следовательно,

(выполняя задания некоторых вариантов необходимо также использовать формулы сокращенного умножения).
2)  Числитель и знаменатель этой дроби стремятся к нулю при
Числитель и знаменатель этой дроби стремятся к нулю при 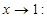
 Для того чтобы вычислить этот предел, необходимо избавиться от иррациональности в числителе. Для этого умножим числитель и знаменатель дроби на сопряженное числителю выражение, получим:
Для того чтобы вычислить этот предел, необходимо избавиться от иррациональности в числителе. Для этого умножим числитель и знаменатель дроби на сопряженное числителю выражение, получим:


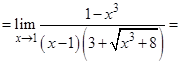


Замечание. Аналогично можно избавляться от иррациональности в знаменателе.
3) 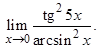 Здесь также имеем неопределенность
Здесь также имеем неопределенность 
В силу первого «замечательного» предела
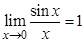 и его следствий
и его следствий 
функции  и
и  ,
,  и
и  ,
, 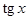 и
и  ,
,  и
и  являются эквивалентными бесконечно малыми при
являются эквивалентными бесконечно малыми при  , т. е.
, т. е.  ~
~  ;
;  ~
~  ;
;  ~
~  ;
;  ~
~  .Следовательно, для этих функций применима теорема: если
.Следовательно, для этих функций применима теорема: если 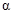 ~
~ 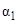 ,
,  ~
~  при
при  и существует
и существует  , то
, то  . Так как при
. Так как при  функции
функции  и
и  ,
,  и
и  — эквивалентные бесконечно малые, т. е. (
— эквивалентные бесконечно малые, т. е. ( ~
~  ,
,  ~
~  ),то
),то 
4)  В таких примерах надо сначала вычислить предел основания степени. Если он отличен от единицы, то выражение не содержит неопределенность, и мы сразу получаем ответ. Если предел основания равен 1, то воспользуемся вторым «замечательным» пределом
В таких примерах надо сначала вычислить предел основания степени. Если он отличен от единицы, то выражение не содержит неопределенность, и мы сразу получаем ответ. Если предел основания равен 1, то воспользуемся вторым «замечательным» пределом  . В нашем случае
. В нашем случае  так как
так как 
Обозначим данный предел какой-нибудь буквой, например, буквой J, и приведем его к виду второго «замечательного» предела с помощью следующего технического приема: к дроби, записанной в скобках, прибавим и вычтем единицу, а затем полученное выражение приведем к общему знаменателю следующим образом:
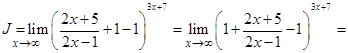



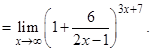 Используем еще один технический прием: возведем выражение в степень
Используем еще один технический прием: возведем выражение в степень  , а потом встепень
, а потом встепень  , чтобы получить вид второго «замечательного» предела
, чтобы получить вид второго «замечательного» предела  .Далее, так как согласно второму «замечательному» пределу
.Далее, так как согласно второму «замечательному» пределу 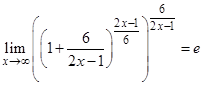 , то
, то  (см. формулу
(см. формулу  ), и, так как
), и, так как  , следовательно, имеем:
, следовательно, имеем: 
5)  В данном примере имеем неопределенность
В данном примере имеем неопределенность  . Разложив знаменатель дроби на множители, приведем данный предел к «замечательному» пределу
. Разложив знаменатель дроби на множители, приведем данный предел к «замечательному» пределу  , в итоге получим:
, в итоге получим: 

 2020-05-25
2020-05-25 129
129








