Точки разрыва функции и их классификация

Точка x ₀, принадлежащая области определения функции f (x) или являющаяся граничной для этой области, называется точкой разрыва функции f (x), если в этой точке нарушается условие непрерывности функции.

Если функция f (x) непрерывна в точке x ₀, то справедливы следующие условия:

1) f (x) определена в точке x ₀, т.е. существует f (x ₀);

2) существует f (x ₀ –) = f (x ₀);

3) существует f (x ₀ +) = f (x ₀).

Если в точке разрыва существуют конечные односторонние пределы f (x ₀ –) и f (x ₀ +), но не выполнено хотя бы одно из условий 1 – 3, то говорят, что в точке x ₀ разрыв I рода. Точки разрыва I рода подразделяются на точки устранимого разрыва, когда f (x ₀ –) = f (x ₀ +) ¹ f (x ₀), и на точки скачка, когда f (x ₀ –) ¹ f (x ₀ +).

Разность f (x ₀ +) – f (x ₀ –) называется скачком функции в точке x ₀.

Если в точке разрыва хотя бы один из односторонних пределов
не существует или бесконечен, то говорят, что в точке x ₀ разрыв II рода.

Функция f (x) называется кусочно-непрерывной на отрезке [ a, b ], если она непрерывна во всех внутренних точках [ a, b ], за исключением, быть может, конечного числа точек, в которых она имеет разрыв I рода,
и в точках x = a, x = b функция f (x) имеет односторонние пределы.

1.4.4 Свойства функций, непрерывных на замкнутом промежутке

Теорема (об ограниченности непрерывной функции, заданной на отрезке): если функция f (x) непрерывна на отрезке [ a, b ], то она ограничена на этом отрезке, т.е. существуют такие два числа A и B, что A £ f (x) £ B для любого x Î [ a, b ].

Теорема (о достижении наименьшего и наибольшего значения непрерывной функции, заданной на отрезке): если функция f (x) непрерывна на отрезке [ a, b ], то на этом отрезке она достигает своего наименьшего и наибольшего значения, т.е. существуют x ₁Î [ a, b ]и x ₂Î [ a, b ] такие, что f (x ₁) £ f (x) £ f (x ₂) для любого x Î [ a, b ].

Теорема (положим 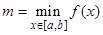, ): если функция f (x) непрерывна на отрезке [ a, b ], то f (x) принимает все промежуточные значения между m и M хотя бы один раз, т.е. для любого числа
C существует точка c Î [ a, b ] такая, что f (c) = C.

Теорема (об обращении непрерывной функции в нуль): пусть функция f (x) непрерывна на отрезке [ a, b ] и на концах отрезка имеет значения разных знаков. Тогда существует точка c Î [ a, b ], для которой f (c) = 0.

Определение: функция f (x) называется равномерно-непрерывной на промежутке (a, b), если для любого e > 0 существует d > 0 такое, что для любых двух точек x ¢, x ² Î (a, b), удовлетворяющих неравенству |x² – x¢| < d, выполняется неравенство .