Эквивалентные бесконечно малые величины

Пусть a(x) ® 0 при х ® х ₀, тогда

1. sin a(x) ~ a(x);       5. ;

2. 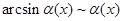;        6. ;

3. ;             7. .

4. ;

Теорема. Пустьa(х) и b(х) суть эквивалентные бесконечно малые величины при

x ® x ₀, т.е.a(х) ~ b(х), x ® x ₀, а f (x) — произвольная функция, тогда пределы  и , либо равны друг другу, либо не существуют. Иными словами, при нахождении предела произведения (или частного) бесконечно малые множители можно заменять эквивалентными величинами.

Теорема. Если a(х) ~ b(х), то a(х) = b(х) + g(х), где  
и , и наоборот, если a(х) = b(х) + g(х), где , то a(х) ~ b(х). Иными словами, для того чтобы две бесконечно малые функции были эквивалентны, необходимо и достаточно, чтобы их разность была бесконечно малой более высокого порядка по сравнению с каждой из них.