Односторонние пределы

Пусть функция 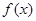определена на промежутке 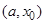. Число A называют пределом функции 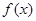в точке 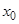слева (или при 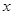стремящемся к 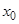слева) и пишут 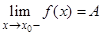, если для любого числа e > 0 можно указать такое число d > 0, зависящее от e, что при всех 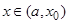, удовлетворяющих неравенству 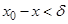, выполняется неравенство .

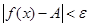Аналогично определяется предел функции 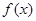в точке 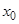справа 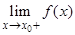для функции 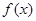, определенной на промежутке 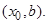Пределы функции слева и справа называют односторонними пределами.

Если функция 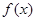определена на промежутке 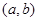, за исключением, быть может, точки 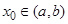, то для существования предела 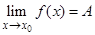необходимо и достаточно, чтобы пределы функции 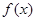в точке 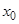слева и справа существовали и были равны: 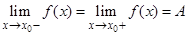.Часто обозначают 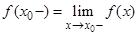и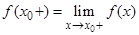

1.3.3 Бесконечно малые и бесконечно большие величины

Функция 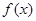называется бесконечно малой величиной при x, стремящемся к x ₀, если 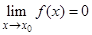. Функция 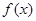называется бесконечно большой величиной при x, стремящемся к x ₀, если для любого числа M > 0 можно указать число d > 0 такое, что при всех x ¹ x ₀, удовлетворяющих неравенству | x – x ₀| < d, выполняется неравенство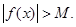

При этом говорят, что функция 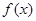стремится к 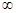и пишут

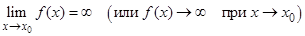Если 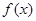— бесконечно большая величина при 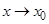, то ее обратная величина 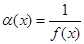— бесконечно малая величина при .

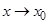Для функций, имеющих предел пр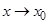и (или 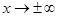), справедливы теоремы, аналогичные теоремам о сходящихся последовательностях (о единственности предела, об ограниченности функции в окрестности предельной точки 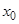, о предельном переходе в неравенстве).

1.3.4 Практическое вычисление пределов

Практическое вычисление пределов основывается на следующей теореме:

Теорема: если существуют пределы функци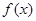й и 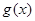в точке 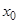, то существуют также пределы суммы и произведения этих функций. При этом

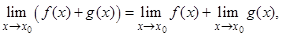
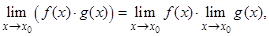
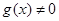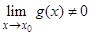если, кроме того, и , то .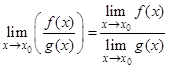

Первый замечательный предел: .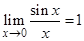

Второй замечательный предел: .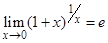

Здесь e = 2,71828 … — основание натуральных логарифмов.

Следствия второго замечательного предела:

; ; .

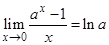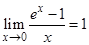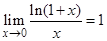Предел элементарной (степенной, показательной, логарифмической, тригонометрических, обратных тригонометрических) функци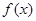и при 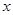, стремящемся к значению 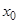, которое входит в область ее определения, равен значению функции при 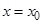, т.е. .

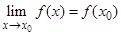1.3.5 Сравнение бесконечно малых и бесконечно больших величин

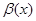Пусть и — бесконечно малые при 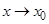(допускается случай ).

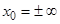1. Если 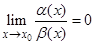, то говорят, что a(х) является бесконечно малой высшего порядка по сравнению с 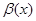при 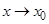и пишут .

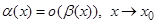Если 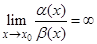, то это означает, что 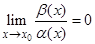, т.е. 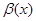является бесконечно малой высшего порядка по сравнению с a(х) при x ® x ₀, .

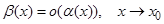2. Если 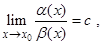где с ¹ 0, то говорят, что a(х) и b(х) — бесконечно малые одного и того же порядка при x ® x ₀. В частности, если 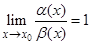, то бесконечно малые a(х) и b(х) называют эквивалентными и пишут a(х) ~ b(х), x ® x ₀.

3. Если 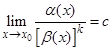, где с ¹ 0, т.е. a(х) и [b(х)]^k — бесконечно малые одного и того же порядка, k ³ 1, то говорят, что функция a(х) — бесконечно малая k-го порядка по сравнению с b(х) при x ® x ₀.