Теорема Ролля (о корнях производной)

Пусть функция  непрерывна на отрезке  и дифференцируема в интервале 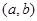. Если 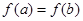, то найдется по крайней мере одна точка , в которой .

Геометрический смысл теоремы Ролля. График функции  имеет в точке (c, f (c)) касательную, параллельную оси OХ (см. рис. 4.3).Между двумя нулями многочлена находится, по крайней мере, один нуль производной этого многочлена .

Теорема Лагранжа (о конечном приращении).

Если функция  задана и непрерывна на отрезке  и дифференцируема в интервале 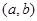, то найдется по крайней мере одна точка , в которой .

Геометрический смысл теоремы Лагранжа. К графику функции  можно провести по крайней мере одну касательную, параллельную секущей, проходящей через точк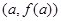и  и  – рис. 4.4. Если  для всех , то

Рис. 4.3	Рис. 4.4

Теорема Коши

Пусть функции  и 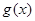 непрерывны на отрезке  и дифференцируемы в интервале  и пусть для всех 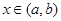. Тогда существует, по крайней мере, одна точка , в которой . Эта формула называется формулой Коши (или обобщенной формулой конечных приращений)

  2.6.3 Решение типовых примеров.

1) Найти производную  функции .

.

Решение

.

2) Найти производную 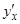 параметрически заданной    функции: .

Решение: Найдем производные от функций  по переменной :

Тогда производная данной функции 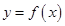 равна:

3) Найти производную 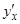 неявно заданной функции      

                       

Решение: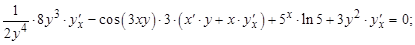   

И окончательно получаем .

4) Найти производную  : .

Логарифмическим дифференцированием называют прием дифференцирования, при котором производная от заданной функции отыскивается с помощью производной от её логарифма. Это значит, что если дана функция , то для нахождения её производной сначала логарифмируют эту функцию , а затем дифференцируют полученное равенство : ,откуда .При логарифмическом дифференцировании удобно применять свойства логарифмов:

                              .

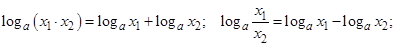
Решние: Прологарифмируем функцию :

отсюда по свойствам логарифмов получаем

Дифференцируем полученное равенство:

Выразив , окончательно получаем: