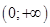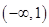Рассмотрим несколько функций и построим их графики.
а)  .
.
Решение: 1. ООФ  ;
;
2. Четность, нечетность: заменим  в выражении, определяющем нашу функцию, на (
в выражении, определяющем нашу функцию, на ( ), получим:
), получим:
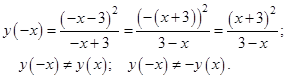
Следовательно, это функция общего вида;
3. Точки пересечения графика с осями координат.
С осью  : на оси
: на оси  имеем
имеем  . Найдем соответствующий этому
. Найдем соответствующий этому
значению аргумента  :
:  Следовательно, график пересекает ось
Следовательно, график пересекает ось
 в точке
в точке  .
.
С осью  : на оси
: на оси  имеем
имеем  . Поэтому получаем
. Поэтому получаем 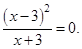
 Следовательно, график пересекает ось
Следовательно, график пересекает ось  в точке с координатами
в точке с координатами  ;
;
4. Непрерывность, точки разрыва. Рассматриваемая функция имеет точку разрыва, так как в точке 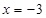 знаменатель функции обращается в ноль. Установим характер указанной точки разрыва
знаменатель функции обращается в ноль. Установим характер указанной точки разрыва  , используя данное ранее определение непрерывности функции в точке:
, используя данное ранее определение непрерывности функции в точке:

Для этого найдем левосторонний и правосторонний пределы. Если  , то, полагая
, то, полагая  , получим:
, получим:
 .
.
Если же  , тогда, полагая
, тогда, полагая  , получаем:
, получаем:

Исходя из наших расчетов, получили следующий результат: левосторонний и правосторонний пределы функции в точке равны бесконечности. В точке  имеем разрыв второго рода;
имеем разрыв второго рода;
5. Асимптоты. Так как в точке  пределы слева и справа равны бесконечности (мы доказали это в предыдущем п. 4), то прямая
пределы слева и справа равны бесконечности (мы доказали это в предыдущем п. 4), то прямая  является вертикальной асимптотой. Найдем наклонную асимптоту
является вертикальной асимптотой. Найдем наклонную асимптоту  . По формулам для асимптот (см. п. 5 в схеме исследования функции), находим
. По формулам для асимптот (см. п. 5 в схеме исследования функции), находим  и
и 

 ;
; 

Значит, прямая  является наклонной асимптотой при
является наклонной асимптотой при  и
и  ;
;
6. Интервалы монотонности и точки экстремума. Для того чтобы найти экстремумы, найдем сначала первую производную нашей функции:

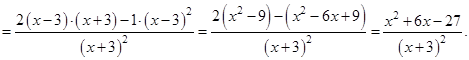
Приравняем первую производную нулю  , тогда
, тогда 
Решая это уравнение, получаем: 


Занесём данные в таблицу, не забыв внести в нее точку разрыва:

| 
| 
| 
| 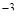
| 
| 
| 
|

| 
| 0 | 
| точка разрыва | 
| 0 | 
|

| 
| –24 max | 
| 
| 0 min | 
|
Функция возрастает на интервалах 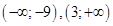 , убывает — на интервале
, убывает — на интервале 
В точке  функция имеет минимум
функция имеет минимум  .
.
В точке  функция имеет максимум
функция имеет максимум  ;
;
7. Интервалы выпуклости, точки перегиба. Для этого найдем вторую производную 


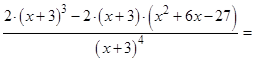

Так как в числителе второй производной стоит постоянное число, то вторая производная не равна нулю ни при каких  . Следовательно, точек перегиба нет. Но мы должны исследовать выпуклость и вогнутость около точки разрыва. Занесем данные в таблицу:
. Следовательно, точек перегиба нет. Но мы должны исследовать выпуклость и вогнутость около точки разрыва. Занесем данные в таблицу:

| 
| 
| 
|

| 
| точка разрыва | 
|

| 
| 
|
8. Для удобства построения и наглядности объединим две таблицы в одну:

| 
| 
| 
| 
| 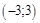
| 
| 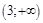
|

| 
| 0 | 
| точка разрыва
| 
| 0 | 
|

| 
| –24 max | 
| 
| 0 min | 
| |
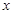
|
|
| |||||

| |
| |||||

| |
| |||||
Построим график функции:

2)  .
.
Решение: Проведем исследование функции по предложенной схеме.
1. ООФ: функция определена везде, т. е. область определения  ;
;
2. Четность, нечетность.  Так как
Так как  функция является функцией общего вида;
функция является функцией общего вида;
3. Точки пересечения графика с осями координат.
С осью  : при
: при 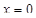 имеем
имеем  , следовательно, график пересекает ось
, следовательно, график пересекает ось  в точке с координатами
в точке с координатами 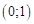 .
.
С осью  : при
: при  имеем
имеем  следовательно, график пересекает ось
следовательно, график пересекает ось  в точке с координатами
в точке с координатами  ;
;
4. Непрерывность, точки разрыва. У данной функции нет никаких точек разрыва, значит, функция непрерывна везде в области определения как произведение непрерывных функций;
5. Асимптоты. Установим наличие вертикальных асимптот. У данной функции нет вертикальных асимптот, так как у неё нет точек разрыва. Найдем наклонные асимптоты. Используем уже известные нам формулы:
 .
.
Имеем неопределенность вида  , для её раскрытия применяем правило Лопиталя:
, для её раскрытия применяем правило Лопиталя:

( ведет себя по-разному при положительном и при отрицательном
ведет себя по-разному при положительном и при отрицательном 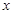 ).
).
При  получаем
получаем  , следовательно, если существует
, следовательно, если существует  , то мы сможем найти асимптоту. Вспомним формулу для
, то мы сможем найти асимптоту. Вспомним формулу для  :
:
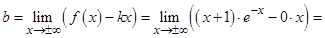

Представим выражение под знаком предела в виде частного и применим правило Лопиталя:

Теперь подставим найденные значения в формулу, получим  . Обращаем внимание на то, что значения
. Обращаем внимание на то, что значения  мы имеем только при положительных
мы имеем только при положительных  . Значит только в этом случае мы имеем частный случай наклонной асимптоты — горизонтальную асимптоту
. Значит только в этом случае мы имеем частный случай наклонной асимптоты — горизонтальную асимптоту  . При отрицательных значениях
. При отрицательных значениях  асимптоты нет, так как в этом случае
асимптоты нет, так как в этом случае  ;
;
6) интервалы монотонности и точки экстремума. Вычислим первую производную функции: 
Приравняем первую производную нулю  , т. е.
, т. е.  Отсюда
Отсюда  . Занесем данные в таблицу:
. Занесем данные в таблицу:

| 
| 0 | 
|

| 
| 0 | 
|

| 
| 1 max | 
|
Производная положительна при  , следовательно, этот интервал является интервалом монотонного возрастания функции. Производная отрицательна при
, следовательно, этот интервал является интервалом монотонного возрастания функции. Производная отрицательна при  , следовательно, этот интервал является интервалом монотонного убывания функции.
, следовательно, этот интервал является интервалом монотонного убывания функции.
 ,таким образом, точка с координатами
,таким образом, точка с координатами 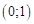 является точкой максимума;
является точкой максимума;
7. Интервалы выпуклости и точки перегиба. Найдем вторую производную:

Далее выясним, при каком значении  вторая производная равна нулю:
вторая производная равна нулю:  так как
так как  при любых значениях
при любых значениях  .
.
Найдем вторую координату возможной точки перегиба  .
.
Исследуем направление выпуклости слева и справа от этой точки. Занесем данные в таблицу:

|

|

|

|

|

| 0 |

|

|

|  точка перегиба
точка перегиба
|

|
Получили, что в этой точке функция действительно меняет направление выпуклости. Значит, точка с координатами 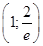 является точкой перегиба
является точкой перегиба  .
.
Для удобства построения и наглядности объединим две таблицы в одну:

|

| 0 |
| |

|

| 0 |
| |

|

|
 max
max
|
| |

|
|

|

| |

|
| 0 |

| |

|
|  точка перегиба
точка перегиба
|

| |
Построим график функции:

3)  .
.
Решение: Проведем исследование функции по предложенной схеме:
1. ООФ: функция существует для всех значений 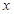 , кроме
, кроме 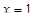 Область определения
Область определения  ;
;
2. Четность, нечетность: 
следовательно, указанная функция — функция общего вида;
3. Точки пересечения графика с осями координат:
 , график пересекает ось
, график пересекает ось  в точке с координатами
в точке с координатами  ;
;
 . Отсюда имеем
. Отсюда имеем  , график пересекает ось
, график пересекает ось  в точке с координатами
в точке с координатами  . Таким образом, точка
. Таким образом, точка  является единственной точкой пересечения и с осью
является единственной точкой пересечения и с осью  и с осью
и с осью  ;
;
4. Непрерывность, точки разрыва. Рассматриваемая функция имеет точку разрыва, так как в точке  знаменатель функции обращается в ноль. Найдем односторонние пределы при
знаменатель функции обращается в ноль. Найдем односторонние пределы при  и
и  тем же способом, что и в предыдущих задачах, считая, что
тем же способом, что и в предыдущих задачах, считая, что  , оставаясь положительной, стремится к нулю:
, оставаясь положительной, стремится к нулю:
 ;
;
 .
.
Мы получили, что левосторонний и правосторонний пределы в данной точке равны бесконечности, следовательно, в точке  имеем разрыв второго рода;
имеем разрыв второго рода;
5. Асимптоты. Так как в точке  предел
предел  , то прямая
, то прямая  является вертикальной асимптотой.
является вертикальной асимптотой.
Найдем наклонную асимптоту  :
:


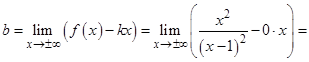


Следовательно, имеем 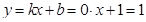 . Значит, прямая
. Значит, прямая  является частным случаем наклонной асимптоты — горизонтальной асимптотой. Прямая
является частным случаем наклонной асимптоты — горизонтальной асимптотой. Прямая  параллельна оси
параллельна оси  ;
;
6. Интервалы монотонности и точки экстремума. Найдем первую производную:


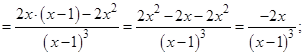
 .
.
В точке  может быть экстремум. Занесем данные в таблицу, не забыв внести в нее точку разрыва:
может быть экстремум. Занесем данные в таблицу, не забыв внести в нее точку разрыва:

| 
| 
| 
| 
| 
|

| 
| 
| 
| точка разрыва | 
|

| 
|  min
min
| 
| 
|
Функция возрастает в интервале  .Функция убывает в интервале
.Функция убывает в интервале  ,
, 
7. Интервалы выпуклости, точки перегиба. Найдем вторую производную:




Вторая производная равна нулю при  . Проверим, является ли эта точка точкой перегиба. Занесем данные в таблицу, не забыв внести в нее точку разрыва:
. Проверим, является ли эта точка точкой перегиба. Занесем данные в таблицу, не забыв внести в нее точку разрыва:

| 
| 
| 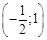
|

| 
|

| 
| 
| 
| точка разрыва
| 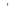
|

| 
| точка
перегиба 
| 
| 
|
Итак, в точке с координатой  имеем перегиб. Найдем вторую координату этой точки:
имеем перегиб. Найдем вторую координату этой точки:  Следовательно, точка перегиба имеет координаты
Следовательно, точка перегиба имеет координаты  .Для удобства построения и наглядности объединим две таблицы в одну:
.Для удобства построения и наглядности объединим две таблицы в одну:

|
| 
| 
| 
| 
| ||

|
| 
| 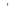
| точка разрыва
| 
| ||

|
|  min min
| 
| ||||

| 
| 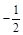
|
| 
| |||

| 
| 0 |
|
| 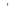
| ||

|

|  точка перегиба точка перегиба
|
|

| |||
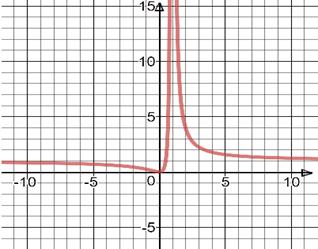
Построим график функции на основе наших результатов:
 2020-05-25
2020-05-25 132
132