1. Определение производной. Геометрический и физический смысл производной.
2. Арифметические свойства производной. Таблица производных.
3. Производная сложной функции. Производные высших порядков.
4. Дифференциал функции. Геометрический смысл дифференциала.
5. Основные теоремы дифференциального исчисления: теоремы Ферма, Ролля, Лагранжа.
6. Правило Лопиталя для раскрытия неопределённостей.
7. Достаточное условие монотонности функции.
8. Экстремумы функции. Необходимое условие экстремума. Достаточное условие экстремума
9. Определение выпуклости вверх и вниз графика функции.
10. Точки перегиба. Необходимый и достаточный признаки точки перегиба графика функции.
2.10 Задачи для проведения промежуточного контроля усвоения материала раздела «Дифференциальное исчисление функции одной переменной.»
Задание 1. Найти производные  заданных функций.
заданных функций.
| 1. | 1) 
| 2) 
|
3) 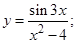
| 4) 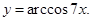
| |
| 2. | 1) 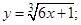
| 2) 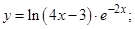
|
3) 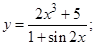
| 4) 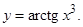
| |
| 3. | 1) 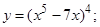
| 2) 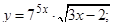
|
3) 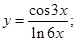
| 4) 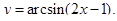
| |
| 4. | 1) 
| 2) 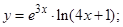
|
3) 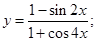
| 4) 
| |
| 5. | 1) 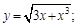
| 2) 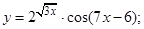
|
3) 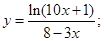
| 4) 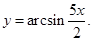
| |
| 6. | 1) 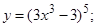
| 2) 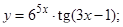
|
3) 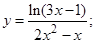
| 4) 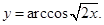
| |
| 7. | 1) 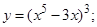
| 2) 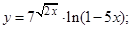
|
3) 
| 4) 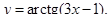
| |
| 8. | 1) 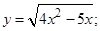
| 2) 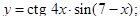
|
3) 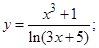
| 4) 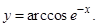
| |
| 9. | 1) 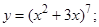
| 2) 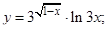
|
3) 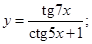
| 4) 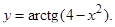
| |
| 10. | 1) 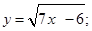
| 2) 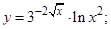
|
3) 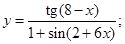
| 4) 
|
Задание 2. 1) Найти интервалы монотонности и точки экстремума,
2) установить интервалы выпуклости и точки перегиба
графика функции 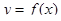 .
.
1. 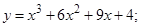
| 2. 
|
3. 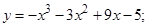
| 7. 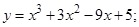
|
5. 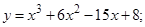
| 8. 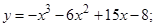
|
4. 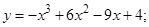
| 9. 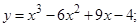
|
5. 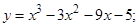
| 10. 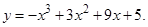
|
Задание 3. С помощью методов дифференциального исчисления исследовать функцию и построить её график.
| 1. | 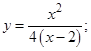
| 2. | 
|
| 3. | 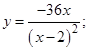
| 4. | 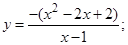
|
| 5. | 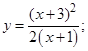
| 6. | 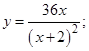
|
| 7. | 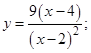
| 8. | 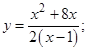
|
| 9. | 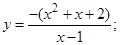
| 10. | 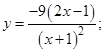
|
Задание 4. Составить уравнение касательной к графику функции 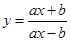
для вариантов 1‒5 в точке с абсциссой 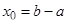 ,
,
для вариантов 6‒10 в точке с абсциссой 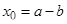 .
.
3. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Цель раздела: изучить теоретический материал раздела «Неопределенный интеграл» и получить практические навыки вычисления неопределенных интегралов методами непосредственного интегрирования, по частям, замены переменных и некоторыми специфическими методами, применимыми к интегралам, содержащими выражения определенного вида.
3.1 Первообразная и неопределенный интеграл
Определение 1.Функция 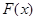 называется первообразной функции
называется первообразной функции 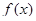 на промежутке
на промежутке 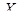 , если она дифференцируема во всех точках этого промежутка и выполняется равенство:
, если она дифференцируема во всех точках этого промежутка и выполняется равенство:
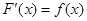 .
. 
Таким образом, первообразная 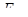 это функция, производная которой равна данной функции
это функция, производная которой равна данной функции 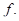 Всякая непрерывная функция
Всякая непрерывная функция  имеет бесчисленное множество различных первообразных функций, которые отличаются друг от друга постоянным слагаемым.
имеет бесчисленное множество различных первообразных функций, которые отличаются друг от друга постоянным слагаемым.
Теорема 1 (об общем виде первообразных).
Пусть 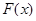 является первообразной для функции
является первообразной для функции 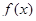 .
.
Для того чтобы другая функция 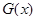 также была первообразной для
также была первообразной для 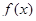 , необходимо и достаточно, чтобы она имела вид:
, необходимо и достаточно, чтобы она имела вид: 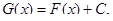 где
где  некоторое число («произвольная постоянная»).
некоторое число («произвольная постоянная»).
Проверим, что 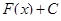 есть также первообразная от
есть также первообразная от
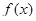 ,
, 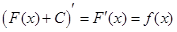 , где
, где 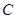 — произвольная постоянная.
— произвольная постоянная.
Определение 2.Пусть функция 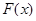 является первообразной для функции
является первообразной для функции 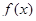 . Тогда выражение
. Тогда выражение 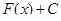 , задающее общий вид всех первообразных, называется неопределенным интегралом от функции
, задающее общий вид всех первообразных, называется неопределенным интегралом от функции 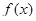 .
.
Термин «неопределенный» связан с тем, что постоянная 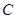 может принимать любое значение. Неопределенный интеграл функции от
может принимать любое значение. Неопределенный интеграл функции от  , обозначается как
, обозначается как 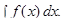
Таким образом, по определению 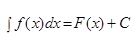 , где
, где  произвольная постоянная.
произвольная постоянная.
Обозначения:
·  — знак неопределенного интеграла;
— знак неопределенного интеграла;
·  — подынтегральная функция;
— подынтегральная функция;
·  — переменная интегрирования;
— переменная интегрирования;
· 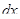 — дифференциал;
— дифференциал;
· 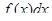 — подынтегральное выражение.
— подынтегральное выражение.
Нахождение первообразной для данной функции 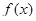 называется интегрированием функции
называется интегрированием функции 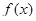 .
.
Интегрирование есть действие, обратное дифференцированию.
Интегрирование производится с помощью основных свойств неопределенного интеграла и таблицы интегралов, приведенных далее.
Таблица интегралов вытекает непосредственно из определения неопределенного интеграла и таблицы производных.
Теорема 2. (достаточное условие существования неопределенного интеграла)
Если функция 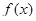 непрерывна на некотором промежутке, то на этом промежутке для нее существует первообразная функция, а значит, и неопределенный интеграл
непрерывна на некотором промежутке, то на этом промежутке для нее существует первообразная функция, а значит, и неопределенный интеграл 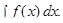
Теорема 3.(равенство неопределенных интегралов).
Два неопределенных интеграла 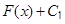 и
и 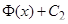 равны, если они задают общий вид первообразных одной и той же функции, то есть если
равны, если они задают общий вид первообразных одной и той же функции, то есть если  .
.
Ø Обратите внимание!
Правильность интегрирования всегдаможнопроверить, выполнив обратное действие, т.е. найдя производную функции, получившейся в результате интегрирования.
Производная должна быть равна подынтегральной функции.
|
3.2 Основные свойства неопределенного интеграла | ||||||||||||||||||||||||||||||||||
I. 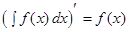 . .
| ||||||||||||||||||||||||||||||||||
II. 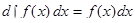 . .
| ||||||||||||||||||||||||||||||||||
III. 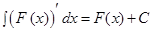
| ||||||||||||||||||||||||||||||||||
IV. 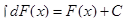
| ||||||||||||||||||||||||||||||||||
| V. VI. | ||||||||||||||||||||||||||||||||||
| 3.3 Таблица интегралов
| ||||||||||||||||||||||||||||||||||
Замечание:Свойства неопределенного интеграла и таблицу интегралов необходимо выучить наизусть.
3.4 Методы непосредственного интегрирования
Прежде чем рассматривать методы интегрирования, научимся применять табличные интегралы. Рассмотрим несколько примеров отыскания интегралов с помощью таблицы и свойств неопределенных интегралов.
Пример 1. Найти интегралы:/”
а) 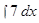 ; б)
; б) 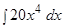 ; в)
; в) 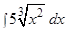 ;
;
г) 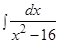 ; д)
; д)  ; е)
; е)  ;
;
Решение:
а) Воспользуемся табличным интегралом (2) и (V) свойством неопределенных интегралов:
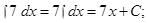
б) Воспользуемся табличным интегралом (1) и (V) свойством неопределенных интегралов:
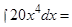
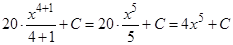 ;
;
в) 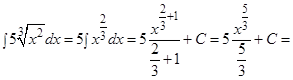
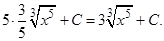
г) Представим  как
как  и воспользуемся табличным интегралом (12), где
и воспользуемся табличным интегралом (12), где  .
.
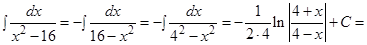
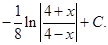
д) Преобразуем выражение в знаменателе и применим формулу (11)
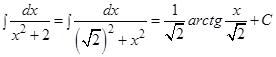 .
.
е) Преобразуем подынтегральную функцию и воспользуемся табличным интегралом
 .
.
Теперь перейдем к методам интегрирования.
3.4.1 Метод разложения
Этот метод применяется для интегрирования функций, представляющих собой алгебраическую сумму нескольких функций, первообразные которых заранее известны или могут быть легко получены.
Рассмотрим примеры.
Пример 2. Найти интегралы:
а) 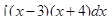 ; б)
; б) 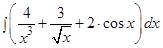 ,в)
,в) 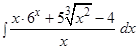 ; г)
; г) 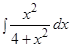 .
.
Решение:
а) 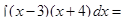
перемножим выражения в скобках и приведем подобные члены в подынтегральном выражении, далее используем формулу (1) таблицы и свойства (IV),(V),(VI).

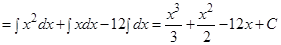 .
.
б)  перейдем к отрицательным степеням и снова представим интеграл как сумму интегралов
перейдем к отрицательным степеням и снова представим интеграл как сумму интегралов
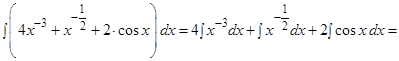
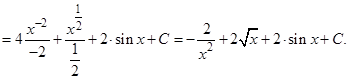
в) Разделим почленно числитель на знаменатель, проведем сокращения и применим табличные интегралы
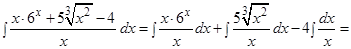
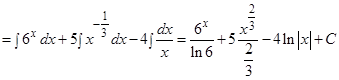
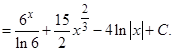
г) Прибавляя и вычитая в числителе 4, получаем
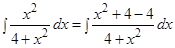
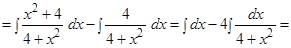
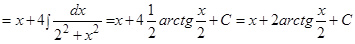
Мы разделили числитель на знаменатель таким образом, чтобы получились табличные интегралы, а потом применили таблицу интегралов.
В основе следующих способов интегрирования лежит свойство инвариантности формул интегрирования, которое заключается в следующем:
Если 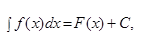 то
то 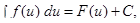
где 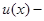 произвольная дифференцируемая функция от
произвольная дифференцируемая функция от  .
.
3.4.2 Внесение постоянного множителя под знак дифференциала.
Согласно определению дифференциала, если 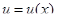
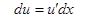 ,
,  тогда
тогда 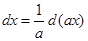 ,
,  и
и  ;
;
Ø Обратите внимание! Интегралы рассмотренные далее однотипны: каждый из них может быть найден путем применения формулы к табличным интегралам.
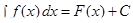


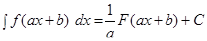
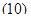
Пример 3. Найти интегралы:
а) 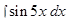 ; б)
; б) 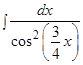 ; в)
; в) 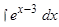 ; г)
; г)  ; д)
; д) 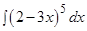 ;
;
е)  ; ж)
; ж) 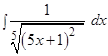 ; з)
; з) 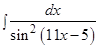 ; и)
; и) 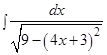 ; к)
; к) 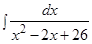 .
.
Решение примеров приведено ниже:
а) 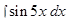 ;
;
Решение: Данный интеграл окажется табличным, если под знаком дифференциала
будет находиться аргумент 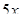 подынтегральной функции
подынтегральной функции 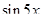
Так как 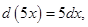 то
то 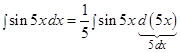 .
.
Следовательно, подстановка 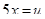 приводит рассматриваемый интеграл к табличному:
приводит рассматриваемый интеграл к табличному:
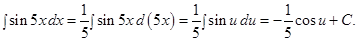
Возвращаясь к старой переменной, окончательно получим 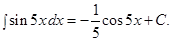
б) 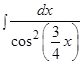
Решение: Проведем преобразования, аналогичные преобразованиям в предыдущем интеграле. Отличие состоит лишь в том, что под дифференциал вносится дробное число.
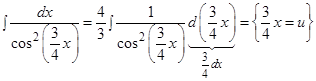

в) 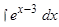 ;
;
Решение: Для того чтобы данный интеграл стал табличным необходимо под знаком дифференциала получить выражение 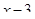 , которое является аргументом подынтегральной функции
, которое является аргументом подынтегральной функции  . Для этого используем формулу
. Для этого используем формулу
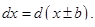
Следовательно, 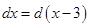 и искомый интеграл имеет вид
и искомый интеграл имеет вид
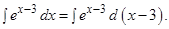
Подстановка 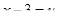 приводит рассматриваемый интеграл к табличному:
приводит рассматриваемый интеграл к табличному:
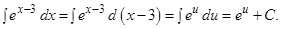
Или, возвращаясь к старой переменной,
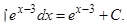
г) 
Решение: В данном примере для преобразования под знаком дифференциалаприменим формулу 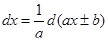 .
.
Так как 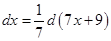 , то
, то 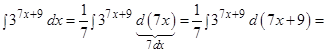
Следовательно, подстановка 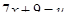 приводит рассматриваемый интеграл к табличному:
приводит рассматриваемый интеграл к табличному:
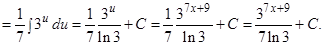
д) 
Решение: Проведем преобразования дифференциала:
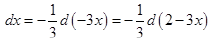
Тогда интеграл приобретает вид:
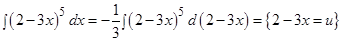
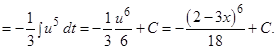
е) 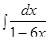
Решение: В данном случае преобразования дифференциала имеют вид:


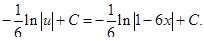
ж) 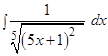
Решение: Имеем 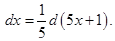 Следовательно,
Следовательно,
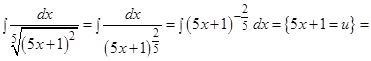
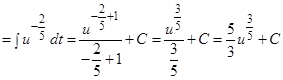
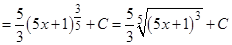 .
.
и) 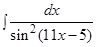
Решение: 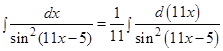

и) 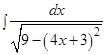
Решение:
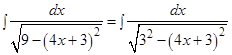
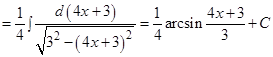
к) 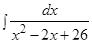 ;
;
Решение: Выделим полный квадрат в знаменателе подынтегральной дроби
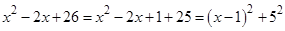 . Тогда,
. Тогда,
 .
.
3.4.3 Внесение переменной под знак дифференциала
Если подынтегральную функцию можно представить как произведение сложной функции 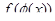 на производную
на производную 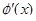 (или функциональную часть этой производной), то замена
(или функциональную часть этой производной), то замена
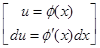

позволяет упростить исходный интеграл, а в простейших случаях свести его к табличному интегралу, т.е.
если 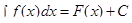 , то
, то 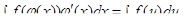
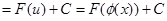

Переход в подынтегральном выражении от записи 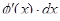 к записи
к записи 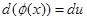 называют внесением множителя
называют внесением множителя 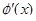 под знак дифференциала. Разумеется (и в этом главная трудность и новизна), нужно научиться в одном из множителей подынтегрального выражения узнавать производную от какой-либо другой его части (пользоваться таблицей производных "в обратную сторону").
под знак дифференциала. Разумеется (и в этом главная трудность и новизна), нужно научиться в одном из множителей подынтегрального выражения узнавать производную от какой-либо другой его части (пользоваться таблицей производных "в обратную сторону").
Пример 4. Найти интегралы:
а) 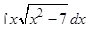 ; б)
; б) 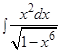 ; в)
; в) 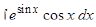 ; г)
; г) 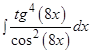 ;
;
а) 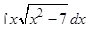 ;
;
Решение:
Для того чтобы решить этот интеграл необходимо под дифференциалом получить 
Замечая, что 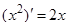 и то, что подынтегральное выражение можно представить в виде
и то, что подынтегральное выражение можно представить в виде
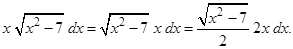
Произведем внесение под знак дифференциала. Для этого выпишем дифференциал:
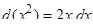 (смотри формулу 11).
(смотри формулу 11).
Более того, 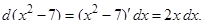 Тогда
Тогда 
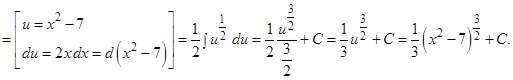
б) 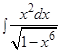 ;
;
Решен: Зная, что 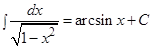 (см. формулу (10) таблицы интегралов), и,узнавая в множителе
(см. формулу (10) таблицы интегралов), и,узнавая в множителе 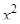 (без множителя 3) производную
(без множителя 3) производную 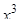 :
: 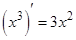 , можем написать:
, можем написать:

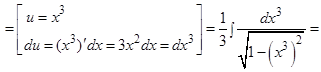
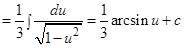
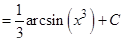 .
.
в) 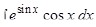 ;
;
Решение: Зная, что  , и, узнавая в множителе
, и, узнавая в множителе  производную
производную 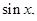 получим
получим


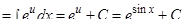 .
.
г) 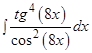 ;
;
Решение: Зная, что 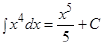 (см. формулу (1) таблицы интегралов), и узнавая в множителе
(см. формулу (1) таблицы интегралов), и узнавая в множителе 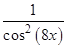 (без множителя 8) производную
(без множителя 8) производную 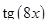 , можем написать:
, можем написать:

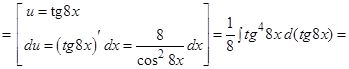
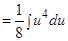
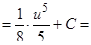
 .
.
В простейших случаях, применяя следующие преобразования дифференциала их возможные комбинации и обозначая мысленно выражение в скобках за новую переменную, интегралы сводятся к табличным.
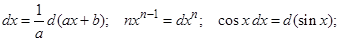
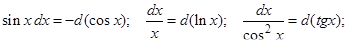
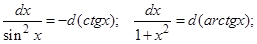
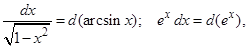
3.5 Интегрирование по частям
Теорема 1. Пусть функции  и
и 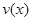 имеют непрерывные производные
имеют непрерывные производные 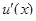 и
и 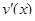 , тогда
, тогда
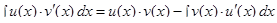
Если в целях краткости записи воспользоваться обозначением дифференциала:
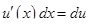 , то формула интегрирования по частям примет вид:
, то формула интегрирования по частям примет вид:
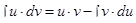

Переход от левой части формулы (15) к правой части оказывается полезен, если для произведения 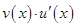 первообразная находится проще, чем для исходного произведения
первообразная находится проще, чем для исходного произведения 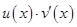 .
.
Применяя интегрирование по частям, нужно разбить подынтегральное выражение на два множителя 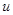 и
и 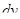 , причем так, чтобы, во-первых, по
, причем так, чтобы, во-первых, по  легко можно было найти
легко можно было найти 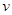 , то есть по
, то есть по 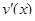 найти первообразную
найти первообразную 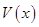 , а во-вторых, чтобы для интеграла в правой части формулы (14) метод отыскания первообразной был известен.
, а во-вторых, чтобы для интеграла в правой части формулы (14) метод отыскания первообразной был известен.
Таким образом, интегрирование по частям проводится в три этапа:
* Подынтегральное выражение разбивается на два множителя 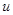 и
и 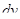 .
.
* По 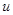 находится
находится 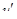 (дифференцированием), а по
(дифференцированием), а по  находится
находится 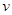 (интегрированием).
(интегрированием).
Отметим, что при переходе от  к
к 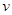 ищется одна какая-либо первообразная без произвольной постоянной
ищется одна какая-либо первообразная без произвольной постоянной 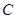 .
.
* Производится переход к правой части формулы (15) и находится интеграл 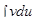
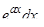
К числу интегралов, вычисляемых по частям, относятся, например, интегралы вида 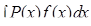 , где
, где 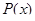 – многочлен.
– многочлен.
Для интегралов вида 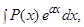
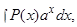
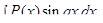
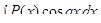 за
за 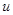 следует принять
следует принять 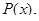 а за
а за  — соответственно выражения
— соответственно выражения 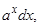
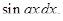
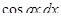 .
.
Для интегралов вида 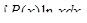

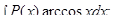
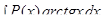 за
за 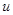 принимаются соответственно функции
принимаются соответственно функции 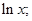
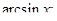
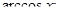
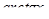 а за
а за  — выражение
— выражение 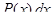
Для интегралов вида 
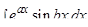 применяется двукратное интегрирование по частям и из полученного выражения определяется исходный интеграл. В этом случае безразлично, что именно принимается за
применяется двукратное интегрирование по частям и из полученного выражения определяется исходный интеграл. В этом случае безразлично, что именно принимается за 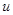 и
и  .
.
Формула интегрирования по частям может применяться неоднократно.
Пример 5. Найти интеграл: 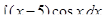
Решение:
Положим 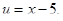
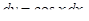 Найдем
Найдем 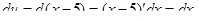
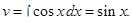
Обычно эти преобразования записывают следующим образом
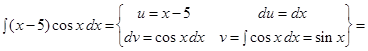
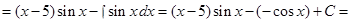
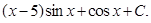
Пример 6. Найти интеграл: 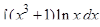
Решение:
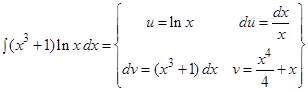
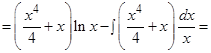
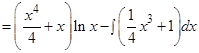


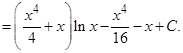
Пример 7. Найти интеграл: 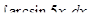 .
.
Решение: 
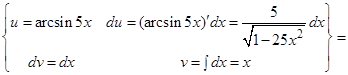
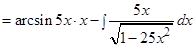
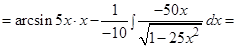
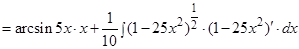
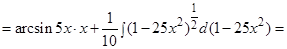
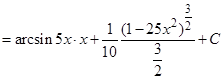
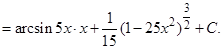
3.6 Замена переменной в неопределенном интеграле
Замена переменной также основана на инвариантности формул интегрирования и позволяет переходить к более простым интегралам.
Пусть переменная интегрирования 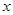 заменяется функцией от новой переменной
заменяется функцией от новой переменной 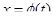 с непрерывной производной
с непрерывной производной 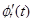 и
и 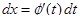 . Тогда
. Тогда


Эта формула называется формулой замены переменной в неопределенном интеграле.
Ø Обратите внимание! В неопределенном интегралепосле операции интегрирования по новой переменной необходимо вернуться к исходной переменной 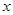 .
.
Пример 8. Найти интегралы: а)  б)
б) 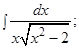 в)
в) 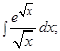 г)
г) 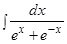 .
.
Решение: а) 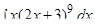 Сделаем замену переменной
Сделаем замену переменной  Отсюда
Отсюда  и
и 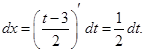 Тогда будем иметь
Тогда будем иметь 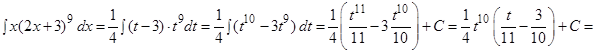
переходя к переменной 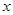 , получим
, получим 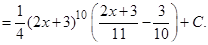
Решение: б) 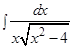 Сделаем замену переменной
Сделаем замену переменной 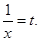 Следовательно,
Следовательно, 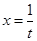 и
и 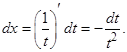 Тогда получим
Тогда получим
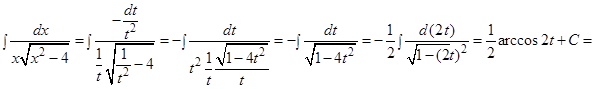
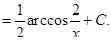
Решение: в) 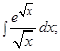 Интеграл
Интеграл 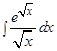 найдем подстановкой
найдем подстановкой 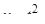 Тогда
Тогда 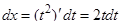 и
и 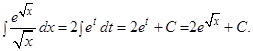
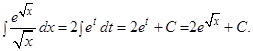 Иногда вместо подстановки
Иногда вместо подстановки  лучше выполнить замену переменной вида
лучше выполнить замену переменной вида 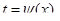
Решение: г) 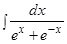 . Полагая
. Полагая  получаем
получаем 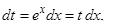 отсюда
отсюда  и
и
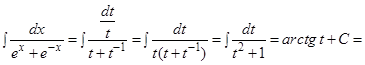

Если подынтегральная функция содержит 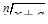 , полезной оказывается подстановка
, полезной оказывается подстановка
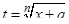 Þ
Þ 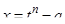

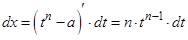

Пример 9. Найти интегралы: a)  ; б)
; б) 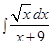 .
.
Решение:
а) 
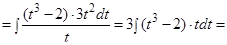
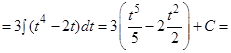
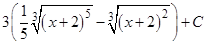 .
.
б) 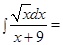
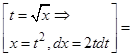
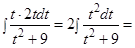
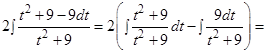
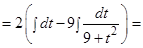
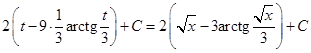 .
.
Пример 10. Найти интеграл: 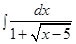 .
.
Решение: В данной подынтегральной функции сделаем подстановку
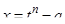

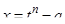

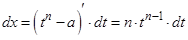
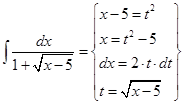


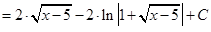 .
.
 2020-05-25
2020-05-25 417
417

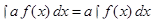 .
.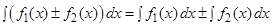 .
.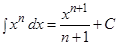 ,
, 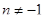 .
.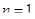
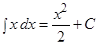
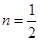
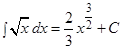
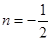
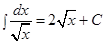
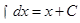 .
.
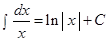 .
.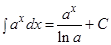 ,
, 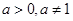
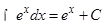 .
. .
.
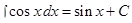 .
. .
.
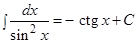 .
.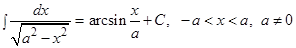
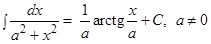 .
.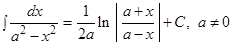 .
.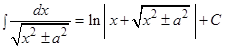 .
.