Различные виды подстановок в неопределенном интеграле

Универсальная тригонометрическая подстановка

Вычисление интегралов типа  осуществляется с помощью подстановки , которая называется универсальной. Действительно,

, , , .

Поэтому получаем .

Другие тригонометрические подстановки

На практике также применяют следующие более простые подстановки:

– если функция  нечетная относительно , т.е. , то делают подстановку ;

– если функция  нечетная относительно , т.е. , то делают подстановку ;

– если функция  четная относительно  и , т.е. , то делают подстановку .

3.8.3 Интегралы типа

Для нахождения таких интегралов используются следующие приемы:

– подстановка , если 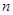— целое положительное нечетное

число;

– подстановка , если — целое положительное нечетное число;

– формулы понижения порядка:

, , ,

если  и 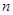 — целые неотрицательные четные числа;

– подстановка , если — четное отрицательное целое число.

Использование тригонометрических преобразований

Интегралы типа , ,  вычисляются с помощью формул тригонометрии:

, ,

.