2020-05-25
190
График функции 
называется выпуклым (вверх)на интервале (a, b), если он расположен ниже касательной, проведенной в любой точке этого интервала (рис. 5.1).
График функции 
называется выпуклым (вниз) на интервале (a, b), если он расположен выше касательной, проведенной в любой точке этого интервала (рис. 5.2).
| 
|
| Рис. 5.1 | Рис. 5.2 |
Правило. Если 
на интервале (a, b), то график функции выпуклый на этом интервале; если же 
, то на интервале (a, b) график функции — вогнутый.
Точка 
графика функции, отделяющая выпуклую его часть от вогнутой, называется точкой перегиба (рис. 5.3).
Если x 0 — абсцисса точки перегиба графика функции 
, вторая производная 
или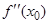 
не существует. Точки, в которых 
и 
не сущест-
вует, называются критическими точками II рода.
|
— критическая точка II рода и при произвольном достаточно малом 
выполняются неравенства 
и 
(или неравенства 
и 
), то точка кривой 
с абсциссой 
является точкой перегиба.
Если же 
и 
имеют одинаковые знаки, то точка кривой 
с абсциссой 
не является точкой перегиба.
Асимптоты
Прямая L называется асимптотой кривой y = f (x), если расстояние точки M с координатами (x, y), лежащей на кривой, от прямой L стремится к нулю при неограниченном удалении указанной точки по кривой от начала координат.
Прямая 
является вертикальной асимптотой кривой , если 
или 
.
Прямая 
является горизонтальной асимптотой кривой y = f (x), если существует конечный предел 
или 
.
Прямая y = kx + b является наклонной асимптотой кривой y = f (x), если существуют конечные пределы:
или 
.
