Контрольные вопросы по разделу «Неопределенный интеграл»

Неопределенный интеграл и его свойства. Теорема существования.
Таблица неопределенных интегралов.
Инвариантность формул интегрирования. Методы непосредственного интегрирования.
Интегрирование по частям для неопределенного интеграла.
Замена переменной в неопределенном интеграле.
Интегрирование рациональных дробей.
Различные виды подстановок в неопределенном интеграле.

3.10 Задачи для проведения промежуточного контроля усвоения материала раздела «Неопределенный интеграл»

Задание 1. Найти неопределенные интегралы.

1. 1)	2. 1)
2)	2)
3)	3)
3. 1)	4. 1)
2)	2)
3)	3)
5. 1)	6. 1)
2)	2)
3)	3)
7. 1)	8. 1)
2)	2)
3)	3)
9. 1)	10.
2)	2)
3)	3)

Задание 2. Вычислить неопределенные интегралы методом интегрирования по частям.

10.

Определенный интеграл

Цель раздела: изучить теоретический материал раздела «Определенный интеграл» и получить практические навыки вычисления определенных интегралов методами непосредственного интегрирования, по частям, замены переменных. Изучить приложения определенного интеграла.

Интегральная сумма и ее предел. Определенный интеграл

Пусть на отрезке определена функция .

Разобьем отрезок на 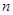произвольных частей точками , выберем на каждом элементарном отрезке произвольную точку и найдем длину каждого такого отрезка: .Вычислим значение функции , а затем составим сумму .

Определение 1. Сумма вида называется интегральной суммой функции на отрезке , соответствующей данному разбиению..

Определение 2. Предел интегральной суммы при условии, что число частичных отрезков неограниченно увеличивается, а длина наибольшего из них стремится к нулю, называется определенным интегралом функции в пределах от до и обозначается

Теорема (условие существования определенного интеграла). Если функция непрерывна на отрезке , то она интегрируема на этом отрезке, то есть предел существует и не зависит от способа разбиения промежутка интегрирования на частичные отрезки и от выбора точек при каждом таком разбиении.