Замена переменной в определенном интеграле

Часто для вычисления интеграла 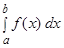 полезно заменить переменную интегрирования  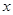новой переменной  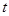при помощи подстановк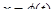и  или 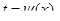 При этом необходимо перейти от старых пределов интегрирования  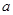и 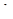 к новым пределам  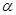и 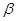, которые определяются из уравнений , .

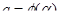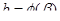Замена переменной осуществляется по формуле

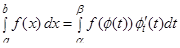
Эта формула справедлива, если 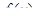 непрерывная функция, а подстановка  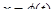сама непрерывна и имеет непрерывную производную на отрезке для всех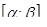  

Ø Обратите внимание! При проведении замены переменной в определенном интеграле следует изменять пределы интегрирования, при этом нет необходимости возвращаться к исходной переменной .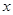

Пример 3. Вычислить определенные интегралы:

       а) 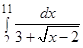,                             б) .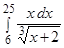

Решение:

а) 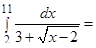Воспользуемся заменой (14) .

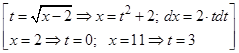Тогда

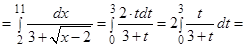
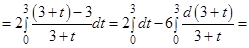
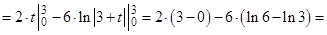
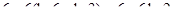
б)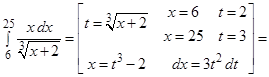

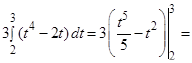
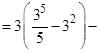
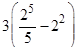
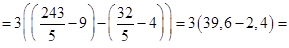
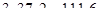
4.4 Приложения определенного интеграла.