-
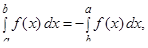
-
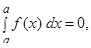
-
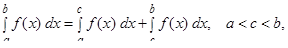
-
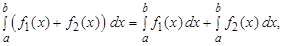
-
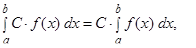 где
где 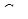 постоянная,
постоянная, - Если
 при
при 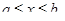 то
то 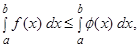
- Если
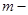 наименьшее, а
наименьшее, а 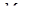 наибольшее значения функции
наибольшее значения функции  на отрезке
на отрезке 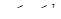 , то
, то 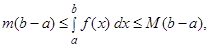
- Теорема о среднем.
Если функция  непрерывна на отрезке
непрерывна на отрезке 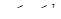 , то на этом отрезке найдется такая точка
, то на этом отрезке найдется такая точка 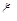 что
что 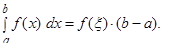 Число
Число 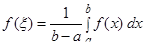 называется средним значением функции
называется средним значением функции  на отрезке
на отрезке 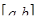
Правила вычисления определенных интегралов.
4.3.1 Формула Ньютона-Лейбница:
При вычислении определенного интеграла следует пользоваться формулой Ньютона-Лейбница.
Эта формула дает удобное правило вычисления определенного интеграла.
Теорема. Если функция 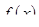 непрерывна на отрезке
непрерывна на отрезке 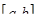 , а
, а 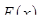 ее произвольная первообразная на этом отрезке, то
ее произвольная первообразная на этом отрезке, то

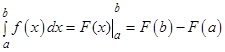
(т.е. определенный интеграл равен разности значений первообразной при верхнем и нижнем пределах интегрирования).
Пример 1. Вычислить определенные интегралы:
а) 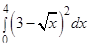 , б)
, б) 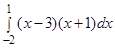 .
.
Решение:
а) 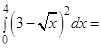 Преобразуем подынтегральную функцию, используя известную формулу квадрата разности:
Преобразуем подынтегральную функцию, используя известную формулу квадрата разности:
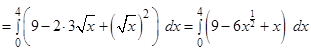 =
= 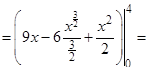
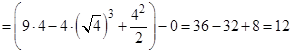
б) 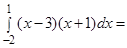
Раскроем скобки и проинтегрируем
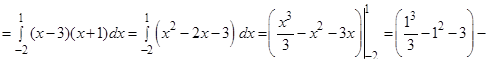
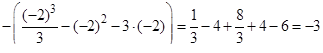 .
.
4.3.2 Интегрирование по частям в определенном интеграле.
Теорема. Если функции 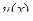 и
и 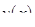 имеют непрерывные производные на отрезке
имеют непрерывные производные на отрезке 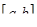 , то справедлива формула интегрирования по частям для определенного интеграла:
, то справедлива формула интегрирования по частям для определенного интеграла:
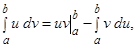

где символ 
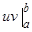 обозначает разность
обозначает разность 
Применение формулы (21) мало чем отличается от применения соответствующей формулы для неопределенного интеграла. Поэтому мы ограничимся приведением примера.
Пример 2. Найти определенный интеграл: 
Решение: Воспользуемся методом интегрирования по частям. Положим 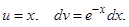 откуда
откуда 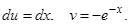 Тогда
Тогда 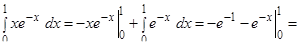
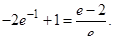
 2020-05-25
2020-05-25 138
138








