2020-05-25
187
Геометрический смысл определенного интеграла: определенный интеграл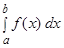 
выражает площадь области, ограниченной кривой 
прямыми 
и осью абсцисс. Такая плоская фигура называется криволинейной трапецией.
Рис. 2
Площадь криволинейной трапеции определяется по формуле: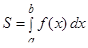 
· Площадь фигуры, образованной пересечением кривых 
, 
и прямыми 
, 
при 
(рис.3), находится по формуле 
.
Рис. 3
· Если кривая задана параметрическими уравнениями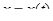 
, 
, то площадь криволинейной трапеции, ограниченной этой кривой и прямыми 
выражается формулой 
, где 
и 
определяются из уравнений 
, 
Рассмотрим несколько примеров на вычисление площадей в прямоугольных
и полярных координатах.
Пример 4. Вычислить площадь фигуры, ограниченной кривыми 
и 
.
Решение: Решение подобных задач необходимо начинать с построения графиков указанных функций и выделения области, площадь которой требуется определить.
Для этого надо найти точки пересечения кривых и 
.
Приравнивая 
, получаем уравнение для определения абсцисс точек пересечения:
, 
откуда 
, 
. Точками пересечения графиков являются точки 
, и 
(Рис. 9).
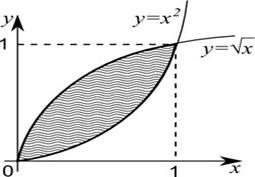
Рис. 5
Далее по формуле находим площадь:
= 
(кв.ед.).
Пример 5. Найти площадь плоской фигуры, ограниченной параболой 
и прямой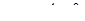 
Решение: Построим график искомой фигуры.
Рис. 6
Затем, решая совместно уравнения, определяющие данные линии, получим
.Отсюда 
и 
Площадь фигуры, ограниченной параболой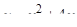 
и прямой 
находим по формуле (29):
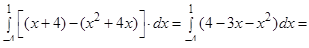
(кв.ед.).
Пример 6. Найти площадь плоской фигуры, ограниченной параболой 
и прямой 
Решение: Построим график искомой фигуры (рис. 7)
Рис. 7
Найдем абсциссы точек пересечения графиков заданных линий:
Получаем 
и 
Искомая площадь равна 
(кв.ед.).
