Интегрирование иррациональных функций

3.8.6 Интегралы типа .

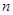Пусть  — многочлен степени . Воспользуемся формулой

,

где Q_{n -1}(x) — многочлен степени n - 1 с неопределенными коэффициентами,  — также неопределенный коэффициент.

Все неопределенные коэффициенты находятся из тождества, получаемого дифференцированием обеих данного частей равенства:

,

после чего необходимо умножить обе части на , привести подобные и для составления системы линейных алгебраических уравнений приравнять коэффициенты при одинаковых степенях .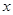

3.8.7 Интегралы вида

Пусть  — целые числа. В таком случае применяется подстановка , где  — общий знаменатель дробей .Аналогично вычисляются и интегралы вида: (  — целые числа), подстановкой , где  — общий знаменатель дробей .

3.8.8 Интегралы вида , ,

Применяются следующие тригонометрические подстановки:  для первого интеграла, x = a tgt для второго интеграла и  — для третьего интеграла.

Интегралы вида  приводятся к предыдущим выделением под радикалом полного квадрата и подстановкой .

3.8.9 Интегралы вида

Такие интегралы, где a, b — действительные числа,  — рациональные числа, называются интегралами от дифференциального бинома  и выражаются через элементарные функции только в следующих трех случаях:

– если 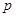— целое число, то применяется подстановка , где k — общий знаменатель дробей  и ;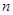

– если  — целое число, то используется подстановка , где  — знаменатель дроби ;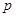

– если  — целое число, то применяется подстановка , где  — знаменатель дроби.